正交(orthogonality)、正交集(orthogonal set)、单位正交集
定义:如果向量 u u u和向量 v v v是相互正交的,则有: u ⋅ v = 0 u\cdot v=0 u⋅v=0。
因为对于零向量,都有 0 T ⋅ v = 0 0^T\cdot v=0 0T⋅v=0,所以零向量与 R n R^n Rn中任意向量正交。
(零向量的默认形式写作 0 = [ 0 0 ⋮ 0 ] 0=\begin{bmatrix}0\\0\\\vdots\\0\end{bmatrix} 0=⎣⎢⎢⎢⎡00⋮0⎦⎥⎥⎥⎤)
R n R^n Rn中的向量集合{ u 1 u_1 u1, … \dots …, u p u_p up}中的任意两个不同的向量都正交,则此集合称为正交集。
如果正交集里面的向量都是单位向量(即长度都为1的向量),则此集合称为单位正交集,
如果单位正交集{ u 1 u_1 u1, … \dots …, u p u_p up}生成子空间H,则{ u 1 u_1 u1, … \dots …, u p u_p up}是H的单位正交基。
最简单的单位正交集是由 R n R^n Rn中的标准基组成的集合 { e 1 , e 2 , … , e n } \{e_1,e_2,\dots,e_n\} { e1,e2,…,en},集合 { e 1 , e 2 , … , e n } \{e_1,e_2,\dots,e_n\} { e1,e2,…,en}的任一非空子集也是单位正交的。
例:
u 1 = [ 3 1 1 ] u_1=\begin{bmatrix}3\\1\\1\end{bmatrix} u1=⎣⎡311⎦⎤, u 2 = [ − 1 2 1 ] u_2=\begin{bmatrix}-1\\2\\1\end{bmatrix} u2=⎣⎡−121⎦⎤, u 3 = [ − 1 2 − 2 7 2 ] u_3=\begin{bmatrix}-\frac{1}{2}\\-2\\\frac{7}{2}\end{bmatrix} u3=⎣⎡−21−227⎦⎤
因为 u 1 ⋅ u 2 = 0 u_1\cdot u_2=0 u1⋅u2=0, u 2 ⋅ u 3 = 0 u_2\cdot u_3=0 u2⋅u3=0, u 1 ⋅ u 3 = 0 u_1\cdot u_3=0 u1⋅u3=0,所以集合{ u 1 u_1 u1, u 2 u_2 u2, u 3 u_3 u3}是正交集。
如果 S = { u 1 , … , u p } S=\{u_1,\dots ,u_p\} S={ u1,…,up}是由 R n R^n Rn中非零向量构成的正交集,则S是线性无关的集合,所以 S = { u 1 , … , u p } S=\{u_1,\dots ,u_p\} S={ u1,…,up}是其所生成的子空间H的一组基。当然,反过来说也成立,即: R n R^n Rn中子空间H的一个正交基不仅是H的一个基,同时也是一个正交集。
定理1:
{ u 1 , … , u p } \{u_1,\dots ,u_p\} { u1,…,up}是由 R n R^n Rn中子空间H的正交基,对H中每个向量 y y y,线性组合 y = c 1 u 1 + ⋯ + c p u p y=c_1u_1+\dots +c_pu_p y=c1u1+⋯+cpup中的权可以用公式 c j = y ⋅ u j u j ⋅ u j c_j=\frac{y\cdot u_j}{u_j\cdot u_j} cj=uj⋅ujy⋅uj来计算。
例:
u 1 = [ 3 1 1 ] u_1=\begin{bmatrix}3\\1\\1\end{bmatrix} u1=⎣⎡311⎦⎤, u 2 = [ − 1 2 1 ] u_2=\begin{bmatrix}-1\\2\\1\end{bmatrix} u2=⎣⎡−121⎦⎤, u 3 = [ − 1 2 − 2 7 2 ] u_3=\begin{bmatrix}-\frac{1}{2}\\-2\\\frac{7}{2}\end{bmatrix} u3=⎣⎡−21−227⎦⎤
由上述例子可知集合{ u 1 u_1 u1, u 2 u_2 u2, u 3 u_3 u3}是正交集,所以也是 R 3 R^3 R3中的一个正交基。请将 y = [ 6 1 − 8 ] y=\begin{bmatrix}6\\1\\-8\end{bmatrix} y=⎣⎡61−8⎦⎤表示成为S中向量的线性组合。
解:
y ⋅ u 1 = 18 + 1 − 8 = 11 y\cdot u_1=18+1-8=11 y⋅u1=18+1−8=11, u 1 ⋅ u 1 = 9 + 1 + 1 = 11 u_1\cdot u_1=9+1+1=11 u1⋅u1=9+1+1=11
y ⋅ u 2 = − 6 + 2 − 8 = − 12 y\cdot u_2=-6+2-8=-12 y⋅u2=−6+2−8=−12, u 2 ⋅ u 2 = 1 + 4 + 1 = 6 u_2\cdot u_2=1+4+1=6 u2⋅u2=1+4+1=6
y ⋅ u 3 = − 3 − 2 − 28 = − 33 y\cdot u_3=-3-2-28=-33 y⋅u3=−3−2−28=−33, u 3 ⋅ u 3 = 1 4 + 4 + 49 4 = 33 2 u_3\cdot u_3=\frac{1}{4}+4+\frac{49}{4}=\frac{33}{2} u3⋅u3=41+4+449=233
由上述定理得:
y = y ⋅ u 1 u 1 ⋅ u 1 ⋅ u 1 + y ⋅ u 2 u 2 ⋅ u 2 ⋅ u 2 + y ⋅ u 3 u 3 ⋅ u 3 ⋅ u 3 = 11 11 u 1 + − 12 6 u 2 + − 33 33 2 u 3 = u 1 − 2 u 2 − 2 u 3 y=\frac{y\cdot u_1}{u_1\cdot u_1}\cdot u_1+\frac{y\cdot u_2}{u_2\cdot u_2}\cdot u_2+\frac{y\cdot u_3}{u_3\cdot u_3}\cdot u_3=\frac{11}{11}u_1+\frac{-12}{6}u_2+\frac{-33}{\frac{33}{2}}u_3=u_1-2u_2-2u_3 y=u1⋅u1y⋅u1⋅u1+u2⋅u2y⋅u2⋅u2+u3⋅u3y⋅u3⋅u3=1111u1+6−12u2+233−33u3=u1−2u2−2u3
总结:由正交基构成的线性表示,如 y = u 1 − 2 u 2 − 2 u 3 y=u_1-2u_2-2u_3 y=u1−2u2−2u3,其中的权( u 1 u_1 u1, u 2 u_2 u2, u 3 u_3 u3前面的数)是较容易由公式算出的。但是如果基不是正交的,则不能用上述公式计算权值,而要用解方程组,然后表示成参数向量形式的方式写出线性表示的式子。
定理2:
一个 m × n m\times n m×n的矩阵 U U U具有单位正交列向量的充要条件是 U T U = I U^TU=I UTU=I。(这个矩阵 U U U如果满足此条件,也叫正交矩阵)
例:矩阵 U = [ 1 2 2 3 1 2 − 2 3 0 1 3 ] U=\begin{bmatrix}\frac{1}{\sqrt{2}}&\frac{2}{3}\\\frac{1}{\sqrt{2}}&-\frac{2}{3}\\0&\frac{1}{3}\end{bmatrix} U=⎣⎡2121032−3231⎦⎤。
对于矩阵 U U U的任两列:
[ 1 2 1 2 0 ] T [ 2 3 − 2 3 1 3 ] = 2 3 − 2 3 + 0 = 0 \begin{bmatrix}\frac{1}{\sqrt{2}}\\\frac{1}{\sqrt{2}}\\0\end{bmatrix}^T \begin{bmatrix}\frac{2}{3}\\-\frac{2}{3}\\\frac{1}{3}\end{bmatrix}=\frac{\sqrt{2}}{3}-\frac{\sqrt{2}}{3}+0=0 ⎣⎡21210⎦⎤T⎣⎡32−3231⎦⎤=32−32+0=0,正交。
且每列的模(即向量的长度,或叫范数)等于1,所以此矩阵具有单位正交列向量。
计算:
U T U = [ 1 2 1 2 0 2 3 − 2 3 1 3 ] [ 1 2 2 3 1 2 − 2 3 0 1 3 ] = [ 1 0 0 1 ] = I U^TU=\begin{bmatrix}\frac{1}{\sqrt{2}}&\frac{1}{\sqrt{2}}&0\\\frac{2}{3}&-\frac{2}{3}&\frac{1}{3}\end{bmatrix} \begin{bmatrix}\frac{1}{\sqrt{2}}&\frac{2}{3}\\\frac{1}{\sqrt{2}}&-\frac{2}{3}\\0&\frac{1}{3}\end{bmatrix}=\begin{bmatrix}1&0\\0&1\end{bmatrix}=I UTU=[213221−32031]⎣⎡2121032−3231⎦⎤=[1001]=I
所以,也可以推出此矩阵具有单位正交列向量。
定理3:
如果矩阵 U U U是一个 m × n m\times n m×n的且具有单位正交列的矩阵,且 x x x和 y y y是 R n R^n Rn中的向量,则:
- ∣ ∣ U x ∣ ∣ = ∣ ∣ x ∣ ∣ ||Ux||=||x|| ∣∣Ux∣∣=∣∣x∣∣
- ( U x ) ⋅ ( U y ) = x ⋅ y (Ux)\cdot (Uy)=x\cdot y (Ux)⋅(Uy)=x⋅y
- ( U x ) ⋅ ( U y ) = 0 (Ux)\cdot (Uy)=0 (Ux)⋅(Uy)=0的充要条件是 x ⋅ y = 0 x\cdot y=0 x⋅y=0.
例:对于上面的矩阵 U = [ 1 2 2 3 1 2 − 2 3 0 1 3 ] U=\begin{bmatrix}\frac{1}{\sqrt{2}}&\frac{2}{3}\\\frac{1}{\sqrt{2}}&-\frac{2}{3}\\0&\frac{1}{3}\end{bmatrix} U=⎣⎡2121032−3231⎦⎤,和 x = [ 2 3 ] x=\begin{bmatrix}\sqrt{2}\\3\end{bmatrix} x=[23],。
由于矩阵 U U U具有单位正交列向量,则:
U x = [ 1 2 2 3 1 2 − 2 3 0 1 3 ] [ 2 3 ] = [ 3 − 1 1 ] Ux=\begin{bmatrix}\frac{1}{\sqrt{2}}&\frac{2}{3}\\\frac{1}{\sqrt{2}}&-\frac{2}{3}\\0&\frac{1}{3}\end{bmatrix}\begin{bmatrix}\sqrt{2}\\3\end{bmatrix}=\begin{bmatrix}3\\-1\\1\end{bmatrix} Ux=⎣⎡2121032−3231⎦⎤[23]=⎣⎡3−11⎦⎤
∣ ∣ U x ∣ ∣ = 9 + 1 + 1 = 11 ||Ux||=\sqrt{9+1+1}=\sqrt{11} ∣∣Ux∣∣=9+1+1=11
∣ ∣ x ∣ ∣ = 2 + 9 = 11 ||x||=\sqrt{2+9}=\sqrt{11} ∣∣x∣∣=2+9=11
即 ∣ ∣ U x ∣ ∣ = ∣ ∣ x ∣ ∣ ||Ux||=||x|| ∣∣Ux∣∣=∣∣x∣∣
总结:
- 如果一个矩阵 U U U可逆,且 U − 1 = U T U^{-1}=U^T U−1=UT,则矩阵 U U U为正交矩阵(orthogonal matrix)。这样的矩阵具有单位正交列。
- 任何具有单位正交列的方阵都是正交矩阵。
- 正交矩阵的每两行也都是单位正交的。
例:
矩阵 U = [ 3 11 − 1 6 − 1 66 1 11 2 6 − 4 66 1 11 1 6 7 66 ] U=\begin{bmatrix}\frac{3}{\sqrt{11}}&-\frac{1}{\sqrt{6}}&-\frac{1}{\sqrt{66}}\\\frac{1}{\sqrt{11}}&\frac{2}{\sqrt{6}}&-\frac{4}{\sqrt{66}}\\\frac{1}{\sqrt{11}}&\frac{1}{\sqrt{6}}&\frac{7}{\sqrt{66}}\end{bmatrix} U=⎣⎢⎡113111111−616261−661−664667⎦⎥⎤
先考察其每两列:
[ 3 11 1 11 1 11 ] T [ − 1 6 2 6 1 6 ] = − 3 66 + 2 66 + 1 66 = 0 \begin{bmatrix}\frac{3}{\sqrt{11}}\\\frac{1}{\sqrt{11}}\\\frac{1}{\sqrt{11}}\end{bmatrix}^T\begin{bmatrix}-\frac{1}{\sqrt{6}}\\\frac{2}{\sqrt{6}}\\\frac{1}{\sqrt{6}}\end{bmatrix}=-\frac{3}{\sqrt{66}}+\frac{2}{\sqrt{66}}+\frac{1}{\sqrt{66}}=0 ⎣⎢⎡113111111⎦⎥⎤T⎣⎢⎡−616261⎦⎥⎤=−663+662+661=0
[ 3 11 1 11 1 11 ] T [ − 1 66 − 4 66 7 66 ] = − 3 11 × 66 − 4 11 × 66 + 7 11 × 66 = 0 \begin{bmatrix}\frac{3}{\sqrt{11}}\\\frac{1}{\sqrt{11}}\\\frac{1}{\sqrt{11}}\end{bmatrix}^T\begin{bmatrix}-\frac{1}{\sqrt{66}}\\-\frac{4}{\sqrt{66}}\\\frac{7}{\sqrt{66}}\end{bmatrix}=-\frac{3}{\sqrt{11\times 66}}-\frac{4}{\sqrt{11\times 66}}+\frac{7}{\sqrt{11\times 66}}=0 ⎣⎢⎡113111111⎦⎥⎤T⎣⎢⎡−661−664667⎦⎥⎤=−11×663−11×664+11×667=0
[ − 1 6 2 6 1 6 ] T [ − 1 66 − 4 66 7 66 ] = 1 6 × 66 − 8 6 × 66 + 7 6 × 66 = 0 \begin{bmatrix}-\frac{1}{\sqrt{6}}\\\frac{2}{\sqrt{6}}\\\frac{1}{\sqrt{6}}\end{bmatrix}^T\begin{bmatrix}-\frac{1}{\sqrt{66}}\\-\frac{4}{\sqrt{66}}\\\frac{7}{\sqrt{66}}\end{bmatrix}=\frac{1}{\sqrt{6\times 66}}-\frac{8}{\sqrt{6\times 66}}+\frac{7}{\sqrt{6\times 66}}=0 ⎣⎢⎡−616261⎦⎥⎤T⎣⎢⎡−661−664667⎦⎥⎤=6×661−6×668+6×667=0
矩阵 U U U的每两列都正交,且每列模为1,所以矩阵 U U U具有单位正交列,所以矩阵 U U U是正交矩阵。
再考察其每两行:
[ 3 11 − 1 6 − 1 66 ] [ 1 11 2 6 − 4 66 ] T = 18 66 − 22 66 + 4 66 = 0 \begin{bmatrix}\frac{3}{\sqrt{11}}&-\frac{1}{\sqrt{6}}&-\frac{1}{\sqrt{66}}\end{bmatrix} \begin{bmatrix}\frac{1}{\sqrt{11}}&\frac{2}{\sqrt{6}}&-\frac{4}{\sqrt{66}}\end{bmatrix}^T=\frac{18}{66}-\frac{22}{66}+\frac{4}{66}=0 [113−61−661][11162−664]T=6618−6622+664=0
[ 3 11 − 1 6 − 1 66 ] [ 1 11 1 6 7 66 ] T = 18 66 − 11 66 − 7 66 = 0 \begin{bmatrix}\frac{3}{\sqrt{11}}&-\frac{1}{\sqrt{6}}&-\frac{1}{\sqrt{66}}\end{bmatrix} \begin{bmatrix}\frac{1}{\sqrt{11}}&\frac{1}{\sqrt{6}}&\frac{7}{\sqrt{66}}\end{bmatrix}^T=\frac{18}{66}-\frac{11}{66}-\frac{7}{66}=0 [113−61−661][11161667]T=6618−6611−667=0
[ 1 11 2 6 − 4 66 ] [ 1 11 1 6 7 66 ] T = 6 66 + 22 66 − 28 66 = 0 \begin{bmatrix}\frac{1}{\sqrt{11}}&\frac{2}{\sqrt{6}}&-\frac{4}{\sqrt{66}}\end{bmatrix} \begin{bmatrix}\frac{1}{\sqrt{11}}&\frac{1}{\sqrt{6}}&\frac{7}{\sqrt{66}}\end{bmatrix}^T=\frac{6}{66}+\frac{22}{66}-\frac{28}{66}=0 [11162−664][11161667]T=666+6622−6628=0
且每行的向量的模也都是1,
所以,可以验证正交矩阵 U U U同样也具有单位正交行。
正交补(Orthocomplement)
如果向量 z z z与 R n R^n Rn的子空间W中的任意向量都正交,则称 z z z正交于W。
与子空间W正交的向量 z z z的全体组成的集合称为W的正交补。
例:直线L垂直于平面W,垂足为O,则L上的所有向量垂直于空间W,所以直线L(向量集合)为W的正交补。反之,W平面空间中所有向量垂直于直线L,所以W也是L空间的正交补。
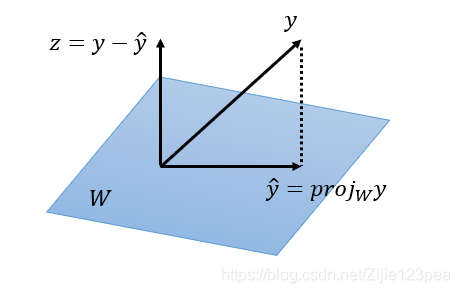
正交分解定理
若W是 R n R^n Rn的一个子空间,那么 R n R^n Rn中每一个向量 y y y可以唯一表示为: y = y ^ + z y=\hat{y}+z y=y^+z
其中 y ^ \hat{y} y^属于W,而 z z z属于W的正交补(即正交于W的空间)。
如果 { u 1 , u 2 , … , u p } \{u_1,u_2,\dots,u_p\} {
u1,u2,…,up}是任意正交基,那么:
y ^ = y ⋅ u 1 u 1 ⋅ u 1 u 1 + ⋯ + y ⋅ u p u p ⋅ u p u p \hat{y}=\frac{y\cdot u_1}{u_1\cdot u_1}u_1+\dots +\frac{y\cdot u_p}{u_p\cdot u_p}u_p y^=u1⋅u1y⋅u1u1+⋯+up⋅upy⋅upup
且 z = y − y ^ z=y-\hat{y} z=y−y^,其中 y ^ \hat{y} y^为 y y y在W上的正交投影,记作 p r o j w y proj_wy projwy。见下图。
例:
设 u 1 = [ 2 5 − 1 ] u_1=\begin{bmatrix}2\\5\\-1\end{bmatrix} u1=⎣⎡25−1⎦⎤, u 2 = [ − 2 1 1 ] u_2=\begin{bmatrix}-2\\1\\1\end{bmatrix} u2=⎣⎡−211⎦⎤, y = [ 1 2 3 ] y=\begin{bmatrix}1\\2\\3\end{bmatrix} y=⎣⎡123⎦⎤,将 y y y写成属于W的向量与正交于W的向量之和。
解:
u 1 ⋅ u 2 = 0 u_1\cdot u_2=0 u1⋅u2=0,所以 { u 1 , u 2 } \{u_1,u_2\} { u1,u2}是 W = S p a n { u 1 , u 2 } W=Span\{u_1,u_2\} W=Span{ u1,u2}的正交基。
由正交分解定理得:
先求 y y y在W上的投影:
y ^ = y ⋅ u 1 u 1 ⋅ u 1 u 1 + y ⋅ u 2 u 2 ⋅ u 2 u 2 = 9 30 [ 2 5 − 1 ] + 3 6 [ − 2 1 1 ] = [ − 2 5 2 1 5 ] \hat{y}=\frac{y\cdot u_1}{u_1\cdot u_1}u_1+\frac{y\cdot u_2}{u_2\cdot u_2}u_2=\frac{9}{30}\begin{bmatrix}2\\5\\-1\end{bmatrix}+\frac{3}{6}\begin{bmatrix}-2\\1\\1\end{bmatrix}=\begin{bmatrix}\frac{-2}{5}\\2\\\frac{1}{5}\end{bmatrix} y^=u1⋅u1y⋅u1u1+u2⋅u2y⋅u2u2=309⎣⎡25−1⎦⎤+63⎣⎡−211⎦⎤=⎣⎡5−2251⎦⎤
再求垂直于W的 z z z( z z z属于W的正交补):
z = y − y ^ = [ 1 2 3 ] − [ − 2 5 2 1 5 ] = [ 7 5 0 14 5 ] z=y-\hat{y}=\begin{bmatrix}1\\2\\3\end{bmatrix}-\begin{bmatrix}\frac{-2}{5}\\2\\\frac{1}{5}\end{bmatrix}=\begin{bmatrix}\frac{7}{5}\\0\\\frac{14}{5}\end{bmatrix} z=y−y^=⎣⎡123⎦⎤−⎣⎡5−2251⎦⎤=⎣⎡570514⎦⎤
所以,可以得到 y y y的分解式是:
y = [ 1 2 3 ] = [ 7 5 0 14 5 ] + [ − 2 5 2 1 5 ] y=\begin{bmatrix}1\\2\\3\end{bmatrix}=\begin{bmatrix}\frac{7}{5}\\0\\\frac{14}{5}\end{bmatrix}+\begin{bmatrix}\frac{-2}{5}\\2\\\frac{1}{5}\end{bmatrix} y=⎣⎡123⎦⎤=⎣⎡570514⎦⎤+⎣⎡5−2251⎦⎤
可见,这样分解出来的两个向量一个是属于W的,另一个是正交与W的。
最佳逼近定理
如果W是 R n R^n Rn的一个子空间, y y y是 R n R^n Rn中任意向量, y ^ \hat{y} y^是 y y y在W上的正交投影,那么 y ^ \hat{y} y^是W中最接近 y y y的点,即有: ∣ ∣ y − y ^ ∣ ∣ < ∣ ∣ y − v ∣ ∣ ||y-\hat{y}||<||y-v|| ∣∣y−y^∣∣<∣∣y−v∣∣对所有属于W,但又异于 y ^ \hat{y} y^的 v v v都成立。
这里的 y ^ \hat{y} y^也叫W中的元素对 y y y的最佳逼近。
例如,在上例中,
y y y在W上的投影:
y ^ = y ⋅ u 1 u 1 ⋅ u 1 u 1 + y ⋅ u 2 u 2 ⋅ u 2 u 2 = 9 30 [ 2 5 − 1 ] + 3 6 [ − 2 1 1 ] = [ − 2 5 2 1 5 ] \hat{y}=\frac{y\cdot u_1}{u_1\cdot u_1}u_1+\frac{y\cdot u_2}{u_2\cdot u_2}u_2=\frac{9}{30}\begin{bmatrix}2\\5\\-1\end{bmatrix}+\frac{3}{6}\begin{bmatrix}-2\\1\\1\end{bmatrix}=\begin{bmatrix}\frac{-2}{5}\\2\\\frac{1}{5}\end{bmatrix} y^=u1⋅u1y⋅u1u1+u2⋅u2y⋅u2u2=309⎣⎡25−1⎦⎤+63⎣⎡−211⎦⎤=⎣⎡5−2251⎦⎤
y ^ \hat{y} y^就是W中距离 y y y最近的点。
由最佳逼近定理可得:从 y y y到W的距离为 ∣ ∣ y − y ^ ∣ ∣ = 49 25 + 196 25 = 49 5 ||y-\hat{y}||=\sqrt{\frac{49}{25}+\frac{196}{25}}=\sqrt{\frac{49}{5}} ∣∣y−y^∣∣=2549+25196=549
( y − y ^ = [ 1 2 3 ] − [ − 2 5 2 1 5 ] = [ 7 5 0 14 5 ] y-\hat{y}=\begin{bmatrix}1\\2\\3\end{bmatrix}-\begin{bmatrix}\frac{-2}{5}\\2\\\frac{1}{5}\end{bmatrix}=\begin{bmatrix}\frac{7}{5}\\0\\\frac{14}{5}\end{bmatrix} y−y^=⎣⎡123⎦⎤−⎣⎡5−2251⎦⎤=⎣⎡570514⎦⎤)
格拉姆-施密特方法(Gram Schmidt method)
方法:对于 R n R^n Rn的子空间W的一个基 { x 1 , x 2 , … , x p } \{x_1,x_2,\dots,x_p\} {
x1,x2,…,xp},定义:
v 1 = x 1 v_1=x_1 v1=x1
v 2 = x 2 − x 2 ⋅ v 1 v 1 ⋅ v 1 v 1 v_2=x_2-\frac{x_2\cdot v_1}{v_1\cdot v_1}v_1 v2=x2−v1⋅v1x2⋅v1v1
v 3 = x 3 − x 3 ⋅ v 1 v 1 ⋅ v 1 v 1 − x 3 ⋅ v 2 v 2 ⋅ v 2 v 2 v_3=x_3-\frac{x_3\cdot v_1}{v_1\cdot v_1}v_1-\frac{x_3\cdot v_2}{v_2\cdot v_2}v_2 v3=x3−v1⋅v1x3⋅v1v1−v2⋅v2x3⋅v2v2
… \dots …
v p = x p − x p ⋅ v 1 v 1 ⋅ v 1 v 1 − x p ⋅ v 2 v 2 ⋅ v 2 v 2 − ⋯ − x p ⋅ v p − 1 v p − 1 ⋅ v p − 1 v p − 1 v_p=x_p-\frac{x_p\cdot v_1}{v_1\cdot v_1}v_1-\frac{x_p\cdot v_2}{v_2\cdot v_2}v_2-\dots -\frac{x_p\cdot v_{p-1}}{v_{p-1}\cdot v_{p-1}}v_{p-1} vp=xp−v1⋅v1xp⋅v1v1−v2⋅v2xp⋅v2v2−⋯−vp−1⋅vp−1xp⋅vp−1vp−1
则 { v 1 , v 2 , … , v p } \{v_1,v_2,\dots,v_p\} {
v1,v2,…,vp}是W的一个正交基。
此外, S p a n { v 1 , … , v k } = S p a n { x 1 , … , x k } Span\{v_1,\dots ,v_k\}=Span\{x_1,\dots ,x_k\} Span{
v1,…,vk}=Span{
x1,…,xk},其中 1 ≤ k ≤ p 1\leq k\leq p 1≤k≤p。
例1:
假设 W = S p a n { x 1 , x 2 } W=Span\{x_1,x_2\} W=Span{
x1,x2},其中 x 1 = [ 3 6 0 ] x_1=\begin{bmatrix}3\\6\\0\end{bmatrix} x1=⎣⎡360⎦⎤, x 2 = [ 1 2 2 ] x_2=\begin{bmatrix}1\\2\\2\end{bmatrix} x2=⎣⎡122⎦⎤,构造 W = S p a n { x 1 , x 2 } W=Span\{x_1,x_2\} W=Span{
x1,x2}的一个正交基。
解:
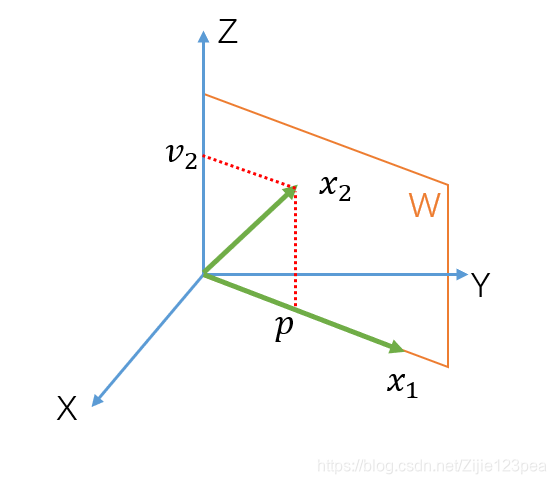
令 v 1 = x 1 v_1=x_1 v1=x1, p p p为 x 2 x_2 x2在 x 1 x_1 x1上的投影。令 v 2 = x 2 − p v_2=x_2-p v2=x2−p为与 x 1 x_1 x1正交的 x 2 x_2 x2的分量, v 2 v_2 v2属于W。
v 2 = x 2 − p = x 2 − x 2 ⋅ x 1 x 1 ⋅ x 1 x 1 = [ 1 2 2 ] − 15 45 [ 3 6 0 ] = [ 0 0 2 ] v_2=x_2-p=x_2-\frac{x_2\cdot x_1}{x_1\cdot x_1}x_1=\begin{bmatrix}1\\2\\2\end{bmatrix}-\frac{15}{45}\begin{bmatrix}3\\6\\0\end{bmatrix}=\begin{bmatrix}0\\0\\2\end{bmatrix} v2=x2−p=x2−x1⋅x1x2⋅x1x1=⎣⎡122⎦⎤−4515⎣⎡360⎦⎤=⎣⎡002⎦⎤
所以 { v 1 , v 2 } \{v_1,v_2\} { v1,v2}是空间W的非零向量构成的正交集,且因为dimW=2,所以 { v 1 , v 2 } \{v_1,v_2\} { v1,v2}是W的一个基,即W的正交基。
标准正交基(Orthonormal Basis):
上例中, v 1 = [ 3 6 0 ] v_1=\begin{bmatrix}3\\6\\0\end{bmatrix} v1=⎣⎡360⎦⎤, v 2 = [ 0 0 2 ] v_2=\begin{bmatrix}0\\0\\2\end{bmatrix} v2=⎣⎡002⎦⎤, { v 1 , v 2 } \{v_1,v_2\} {
v1,v2}是W的正交基,把它变成标准正交基,即把每个元素单位化即可:
u 1 = v 1 ∣ ∣ v 1 ∣ ∣ = 1 45 [ 3 6 0 ] = [ 1 5 2 5 0 ] u_1=\frac{v_1}{||v_1||}=\frac{1}{\sqrt{45}}\begin{bmatrix}3\\6\\0\end{bmatrix}=\begin{bmatrix}\frac{1}{\sqrt{5}}\\\frac{2}{\sqrt{5}}\\0\end{bmatrix} u1=∣∣v1∣∣v1=451⎣⎡360⎦⎤=⎣⎡51520⎦⎤
u 2 = v 2 ∣ ∣ v 2 ∣ ∣ = 1 4 [ 0 0 2 ] = [ 0 0 1 ] u_2=\frac{v_2}{||v_2||}=\frac{1}{\sqrt{4}}\begin{bmatrix}0\\0\\2\end{bmatrix}=\begin{bmatrix}0\\0\\1\end{bmatrix} u2=∣∣v2∣∣v2=41⎣⎡002⎦⎤=⎣⎡001⎦⎤
{ u 1 , u 2 } \{u_1,u_2\} { u1,u2}是W的标准正交基。
例2:
设 x 1 = [ 1 1 1 1 ] x_1=\begin{bmatrix}1\\1\\1\\1\end{bmatrix} x1=⎣⎢⎢⎡1111⎦⎥⎥⎤, x 2 = [ 0 1 1 1 ] x_2=\begin{bmatrix}0\\1\\1\\1\end{bmatrix} x2=⎣⎢⎢⎡0111⎦⎥⎥⎤, x 3 = [ 0 0 1 1 ] x_3=\begin{bmatrix}0\\0\\1\\1\end{bmatrix} x3=⎣⎢⎢⎡0011⎦⎥⎥⎤,请构造 R 4 R^4 R4子空间W的一个正交基。
解:
由于 { x 1 , x 2 , x 3 } \{x_1,x_2,x_3\} { x1,x2,x3}是线性无关的,所以它们构成W的一个基。
先令 v 1 = x 1 v_1=x_1 v1=x1, W 1 = S p a n { x 1 } = S p a n { v 1 } W_1=Span\{x_1\}=Span\{v_1\} W1=Span{ x1}=Span{ v1}
再取 v 2 v_2 v2等于 x 2 x_2 x2减去它在子空间 W 1 W_1 W1上投影所得的向量,即:
v 2 = x 2 − p v_2=x_2-p v2=x2−p为与 x 1 x_1 x1正交的 x 2 x_2 x2的分量, v 2 v_2 v2属于W,且 { v 1 , v 2 } \{v_1,v_2\} {
v1,v2}是由 x 1 x_1 x1, x 2 x_2 x2所生成的子空间 W 2 W_2 W2的一个正交基。
v 2 = x 2 − p r o j W 1 x 2 = x 2 − x 2 ⋅ v 1 v 1 ⋅ v 1 v 1 = [ 0 1 1 1 ] − 3 4 [ 1 1 1 1 ] = [ − 3 4 1 4 1 4 1 4 ] v_2=x_2-proj_{W_1}x_2=x_2-\frac{x_2\cdot v_1}{v_1\cdot v_1}v_1=\begin{bmatrix}0\\1\\1\\1\end{bmatrix}-\frac{3}{4}\begin{bmatrix}1\\1\\1\\1\end{bmatrix}=\begin{bmatrix}-\frac{3}{4}\\\frac{1}{4}\\\frac{1}{4}\\\frac{1}{4}\end{bmatrix} v2=x2−projW1x2=x2−v1⋅v1x2⋅v1v1=⎣⎢⎢⎡0111⎦⎥⎥⎤−43⎣⎢⎢⎡1111⎦⎥⎥⎤=⎣⎢⎢⎡−43414141⎦⎥⎥⎤
当然,可以吧 v 2 v_2 v2的分数放缩成整数:
v 1 = [ 1 1 1 1 ] v_1=\begin{bmatrix}1\\1\\1\\1\end{bmatrix} v1=⎣⎢⎢⎡1111⎦⎥⎥⎤, v 2 ′ = 4 v 2 = [ − 3 1 1 1 ] v_2^{'}=4v_2=\begin{bmatrix}-3\\1\\1\\1\end{bmatrix} v2′=4v2=⎣⎢⎢⎡−3111⎦⎥⎥⎤
再取 v 3 v_3 v3是 x 3 x_3 x3减去它在子空间 W 2 W_2 W2上的投影所得的向量:
先用正交基 { v 1 , v 2 ′ } \{v_1,v_2^{'}\} { v1,v2′}计算 x 3 x_3 x3在 W 2 W_2 W2上的投影:
p r o j W 2 x 3 = p r o j v 1 x 3 + p r o j v 2 ′ x 3 = x 3 ⋅ v 1 v 1 ⋅ v 1 v 1 + x 3 ⋅ v 2 ′ v 2 ′ ⋅ v 2 ′ v 2 ′ = 2 4 [ 1 1 1 1 ] + 2 12 [ − 3 1 1 1 ] = [ 0 2 3 2 3 2 3 ] proj_{W_2}x_3=proj_{v_1}x_3+proj_{v_2^{'}}x_3= \frac{x_3\cdot v_1}{v_1\cdot v_1}v_1+\frac{x_3\cdot v_2^{'}}{v_2^{'}\cdot v_2^{'}}v_2^{'}=\frac{2}{4}\begin{bmatrix}1\\1\\1\\1\end{bmatrix}+\frac{2}{12}\begin{bmatrix}-3\\1\\1\\1\end{bmatrix}=\begin{bmatrix}0\\\frac{2}{3}\\\frac{2}{3}\\\frac{2}{3}\end{bmatrix} projW2x3=projv1x3+projv2′x3=v1⋅v1x3⋅v1v1+v2′⋅v2′x3⋅v2′v2′=42⎣⎢⎢⎡1111⎦⎥⎥⎤+122⎣⎢⎢⎡−3111⎦⎥⎥⎤=⎣⎢⎢⎡0323232⎦⎥⎥⎤
那么 v 3 v_3 v3是 x 3 x_3 x3正交于 W 2 W_2 W2的分量,即:
v 3 = x 3 − p r o j W 2 x 3 = [ 0 0 1 1 ] − [ 0 2 3 2 3 2 3 ] = [ 0 − 2 3 1 3 1 3 ] v_3=x_3-proj_{W_2}x_3=\begin{bmatrix}0\\0\\1\\1\end{bmatrix}-\begin{bmatrix}0\\\frac{2}{3}\\\frac{2}{3}\\\frac{2}{3}\end{bmatrix}=\begin{bmatrix}0\\-\frac{2}{3}\\\frac{1}{3}\\\frac{1}{3}\end{bmatrix} v3=x3−projW2x3=⎣⎢⎢⎡0011⎦⎥⎥⎤−⎣⎢⎢⎡0323232⎦⎥⎥⎤=⎣⎢⎢⎡0−323131⎦⎥⎥⎤
所以 { v 1 , v 2 ′ , v 3 } \{v_1,v_2^{'},v_3\} { v1,v2′,v3}是W的正交基。
QR分解
定理:如果 m × n m\times n m×n的矩阵 A A A各列线性无关,那么 A A A可以分解为 A = Q R A=QR A=QR,其中 Q Q Q为一个 m × n m\times n m×n的矩阵,其各列形成Col A的一个标准正交基, R R R是一个 n × n n\times n n×n的上三角可逆矩阵,且在对角线上的元素为正数。
例:
求矩阵 A = [ 1 0 0 1 1 0 1 1 1 1 1 1 ] A=\begin{bmatrix}1&0&0\\1&1&0\\1&1&1\\1&1&1\end{bmatrix} A=⎣⎢⎢⎡111101110011⎦⎥⎥⎤的一个QR分解。
矩阵 A A A的列向量同上面例2的列向量:
x 1 = [ 1 1 1 1 ] x_1=\begin{bmatrix}1\\1\\1\\1\end{bmatrix} x1=⎣⎢⎢⎡1111⎦⎥⎥⎤, x 2 = [ 0 1 1 1 ] x_2=\begin{bmatrix}0\\1\\1\\1\end{bmatrix} x2=⎣⎢⎢⎡0111⎦⎥⎥⎤, x 3 = [ 0 0 1 1 ] x_3=\begin{bmatrix}0\\0\\1\\1\end{bmatrix} x3=⎣⎢⎢⎡0011⎦⎥⎥⎤
C o l A = S p a n { x 1 , x 2 , x 3 } Col\space A=Span\{x_1,x_2,x_3\} Col A=Span{
x1,x2,x3}的一个正交基在上面例2中求得为:
v 1 = [ 1 1 1 1 ] v_1=\begin{bmatrix}1\\1\\1\\1\end{bmatrix} v1=⎣⎢⎢⎡1111⎦⎥⎥⎤, v 2 ′ = [ − 3 1 1 1 ] v_2^{'}=\begin{bmatrix}-3\\1\\1\\1\end{bmatrix} v2′=⎣⎢⎢⎡−3111⎦⎥⎥⎤, v 3 = [ 0 − 2 3 1 3 1 3 ] v_3=\begin{bmatrix}0\\-\frac{2}{3}\\\frac{1}{3}\\\frac{1}{3}\end{bmatrix} v3=⎣⎢⎢⎡0−323131⎦⎥⎥⎤
重新度量 v 3 v_3 v3,取 v 3 ′ = 3 v 3 = [ 0 − 2 1 1 ] v_3^{'}=3v_3=\begin{bmatrix}0\\-2\\1\\1\end{bmatrix} v3′=3v3=⎣⎢⎢⎡0−211⎦⎥⎥⎤
将 v 1 v_1 v1, v 2 ′ v_2^{'} v2′和 v 3 ′ v_3^{'} v3′单位化:
u 1 = v 1 ∣ ∣ v 1 ∣ ∣ = 1 4 [ 1 1 1 1 ] = [ 1 2 1 2 1 2 1 2 ] u_1=\frac{v_1}{||v_1||}=\frac{1}{\sqrt{4}}\begin{bmatrix}1\\1\\1\\1\end{bmatrix}=\begin{bmatrix}\frac{1}{2}\\\frac{1}{2}\\\frac{1}{2}\\\frac{1}{2}\end{bmatrix} u1=∣∣v1∣∣v1=41⎣⎢⎢⎡1111⎦⎥⎥⎤=⎣⎢⎢⎡21212121⎦⎥⎥⎤
u 2 = v 2 ′ ∣ ∣ v 2 ′ ∣ ∣ = 1 12 [ − 3 1 1 1 ] = [ − 3 12 1 12 1 12 1 12 ] u_2=\frac{v_2^{'}}{||v_2^{'}||}=\frac{1}{\sqrt{12}}\begin{bmatrix}-3\\1\\1\\1\end{bmatrix}=\begin{bmatrix}-\frac{3}{\sqrt{12}}\\\frac{1}{\sqrt{12}}\\\frac{1}{\sqrt{12}}\\\frac{1}{\sqrt{12}}\end{bmatrix} u2=∣∣v2′∣∣v2′=121⎣⎢⎢⎡−3111⎦⎥⎥⎤=⎣⎢⎢⎢⎡−123121121121⎦⎥⎥⎥⎤
u 3 = v 3 ′ ∣ ∣ v 3 ′ ∣ ∣ = 1 6 [ 0 − 2 1 1 ] = [ 0 − 2 6 1 6 1 6 ] u_3=\frac{v_3^{'}}{||v_3^{'}||}=\frac{1}{\sqrt{6}}\begin{bmatrix}0\\-2\\1\\1\end{bmatrix}=\begin{bmatrix}0\\-\frac{2}{\sqrt{6}}\\\frac{1}{\sqrt{6}}\\\frac{1}{\sqrt{6}}\end{bmatrix} u3=∣∣v3′∣∣v3′=61⎣⎢⎢⎡0−211⎦⎥⎥⎤=⎣⎢⎢⎢⎡0−626161⎦⎥⎥⎥⎤
根据QR分解定理: Q Q Q矩阵是待分解矩阵 A A A的列空间的标准正交基,所以:
Q = [ u 1 u 2 u 3 ] = [ 1 2 − 3 12 0 1 2 1 12 − 2 6 1 2 1 12 1 6 1 2 1 12 1 6 ] Q=[u_1\quad u_2\quad u_3]=\begin{bmatrix}\frac{1}{2}&-\frac{3}{\sqrt{12}}&0\\\frac{1}{2}&\frac{1}{\sqrt{12}}&-\frac{2}{\sqrt{6}}\\\frac{1}{2}&\frac{1}{\sqrt{12}}&\frac{1}{\sqrt{6}}\\\frac{1}{2}&\frac{1}{\sqrt{12}}&\frac{1}{\sqrt{6}}\end{bmatrix} Q=[u1u2u3]=⎣⎢⎢⎢⎡