[题解]CF1525D Armchairs dp

有一排座位，编号$1n$，其中不超过$\frac{n}{2}$的座位被人坐上了。
现在需要调整每个人的座位，每次把坐在i的人调到空位j的代价是$|i-j|$。
现在需要把每个人调一次，使得原来坐了人的位置都空出来。问最小的花费是多少。
刚开始想的是贪心。用$a,b$分别记录人和空位的下标，然后升序排序，最后从左到右依次遍历。可惜的是，这种算法只对$n$是偶数并且出现的人正好有$\frac{n}{2}$时才适用。虽然错了，但这个思路很好。
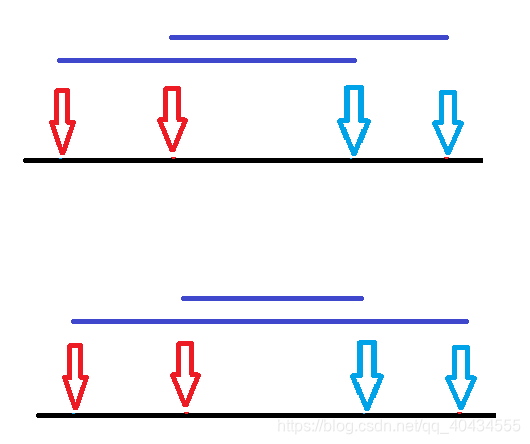
从左到右，对于每一个$a_i$，我们匹配$b_i$(即当下最小的)。这样的话，对于每一个$a_i<a_j$，$b_i<b_j$，都会出现4种情况。
$①.$
$②.$

$③.$

这三种情况显然满足。
$④.$
可以看出，此处对于每个$a$,选择最小的$b$不会排除最优解。
虽然这个算法对此题不适用，但是我们仍然能够得到一些有用的结论。
对于$a_i<a_j$，$a_i$所选择的$b_{t_i}$必然比$a_j$所选择的$b_{t_j}$小。
因此我们可以用动态规划。
设$dp[i][j]$表示用前$i$个人去匹配前$j$个空位的最小代价，那么我们容易得出$$dp[i][j]=min\left(dp\right[i-1][k])+\left|a[i]-b[j]\right|,1\le k<b[j]$$
对于$min\left(dp[i-1][k]\right)$，它是一个前缀最小值，我们可以用一个$minx$数组记录。这样时间复杂度就从$O(n^3)$降到了$O(n^2)$。
有些小的坑点都写在代码段里了。

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<string>
#include<cmath>
#include<algorithm>
#include<vector>
#include<map>
#include<queue>
#include<stack>
#define ll long long
#define pii pair<int,int>
using namespace std;

const double eps = 1e-10;
const double pi = acos(-1.0);
const int maxn = 5010;

int n;
int x[maxn];
int a[maxn],b[maxn];
ll dp[maxn][maxn];
ll minx[maxn][maxn];
void solve(){
    
      
	scanf("%d",&n);
	for(int i = 1; i <= n; i++){
    
      
		scanf("%d",&x[i]);
		if(x[i]) a[++a[0]] = i;
		else b[++b[0]] = i;
	}
	sort(a+1,a+a[0]+1);
	sort(b+1,b+b[0]+1);
	for(int i = 1; i <= a[0]; i++){
    
      
		for(int j = i; j <= b[0]; j++){
    
      
		//注意，这里j至少从i开始，因为如果选到更加前面的数，那么就会重复，产生错误。
			dp[i][j] = minx[i-1][j-1] + (ll)abs(a[i]-b[j]);
			if(j == i) minx[i][j] = dp[i][j];
			else minx[i][j] = min(minx[i][j-1],dp[i][j]);
		}
	}
	ll ans = 1145141919810;
	for(int i = 1; i <= n; i++) if(dp[a[0]][i]) ans = min(ans,dp[a[0]][i]);
	if(ans == 1145141919810) ans = 0;//有可能一个人也没有
	printf("%lld\n",ans);
}

int main()
{
    
      
	solve();
	return 0;
}

另外，对于这个式子，其实还有其他的转移方法。我们考虑最后一个人$i$与当前这个空位$j$是否匹配。如果匹配，那么答案贡献就是$dp[i-1][j-1]+\left|a[i]-b[j]\right|$；否则不选，我们就在前$j-1$个空位中选择，答案贡献即为$dp[i][j-1]$，故
$$dp[i][j]=min\left(dp[i-1][j-1]+\left|a[i]-b[j]\right|,dp[i][j-1]\right)$$
感觉就是个LCS，为什么考场上没有想到呢(悲)