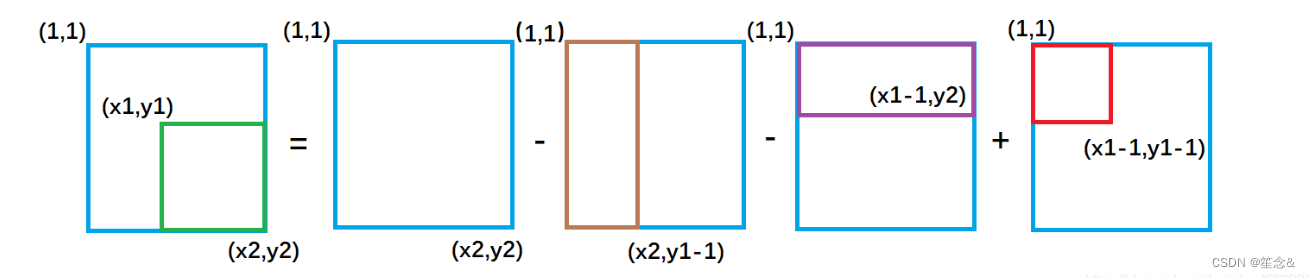目录
一 前缀和
算法定义
定义:
前缀和是指某序列的前n项和,可以把它理解为数学上的数列的前n项和
一个长度为n的数组a[0] - a[n-1],他的前缀和sum[i]等于a[0] - a[i]的和
利用递推可以在O(n)时间内球的所有前缀和:sum[i] =sum[i-1] +a[i]
算法分类
算法作用
如果预计算出前缀和,就能利用他快速计算出数组中任意区间a[i] - a[j]的和,即
a[i]+a[i+1]+...+a[j-1]+a[j]=sum[j]-sum[i-1]
这说明复杂度为O(n)的区间和计算优化到了O(1)的前缀和计算
一维前缀和
问题引入
输入一个长度为n的整数序列。接下来再输入m个询问,每个询问输入一对l, r。对于每个询问,输出原序列中从第l个数到第r个数的和。
暴力法:
const int N = 1e5 + 10;
int a[N];
int n,m;
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i++) scanf("%d", &a[i]);
while(m--)
{
int l, r;
int sum = 0;
scanf("%d%d", &l, &r);
for(int i = l; i <= r; i++)
{
sum += a[i];
}
printf("%d\n",sum);
}
时间复杂度O(n*m)
前缀和法:
①首先做一个预处理,定义一个sum[]数组,sum[i]代表a数组中前i个数的和
②求前缀和运算://预处理操作
const int N = 1e5 + 10;
int sum[N], a[N]; //sum[i]=a[1]+a[2]+a[3].....a[i];
for(int i = 1;i <= n; i++)
{
sum[i] = sum[i - 1] + a[i];
}
③查询操作
scanf("%d%d",&l,&r);
printf("%d\n", sum[r] - sum[l - 1]);
对于每次查询,只需执行sum[r] - sum[l - 1] ,时间复杂度为O(1)
算法原理
sum[r] = a[1] + a[2] + a[3] + a[l-1] + a[l] + a[l + 1] ...... a[r];
sum[l - 1] = a[1] + a[2] + a[3] + a[l - 1];
sum[r] - sum[l - 1] = a[l] + a[l + 1] + ......+ a[r];
这样,对于每个询问,只需要执行 sum[r] - sum[l - 1]。输出原序列中从第l个数到第r个数的和的时间复杂度变成了O(1)。
我们把它叫做一维前缀和
问题解答
#include <iostream>
using namespace std;
const int N = 100010;
int n, m;
int a[N], s[N];
int main()
{
scanf("%d%d", &n, &m);
for (int i = 1; i <= n; i ++ ) scanf("%d", &a[i]);
for (int i = 1; i <= n; i ++ ) s[i] = s[i - 1] + a[i]; // 前缀和的初始化
while (m -- )
{
int l, r;
scanf("%d%d", &l, &r);
printf("%d\n", s[r] - s[l - 1]); // 区间和的计算
}
return 0;
}
算法实践
江山白日梦
题目描述
小江又在做白日梦了,她进入到她的幻想中,发现她的对象帮她打下了一片江山
打下的江山一共有 n 个城市,城市i和城市i+ 1有一条双向高速公路连接,走这条路要耗费时间ai
为了关心人民生活,小江决定定期进行走访。她每一次会从1号城市到 n 号城市并在经过的城市进
行访问。其中终点必须为城市 n
不仅如此,她对象还给她准备了一个传送器,传送半径为k,也就是可以传送到 i- k 和i+k。如果目
标城市编号小于1则为 1,大于n则为n。
但是她的传送器电量不足,只能传送一次,况且由于一些原因,她想尽量快的完成访问,于是就想
问交通部部长您最快的时间是多少。
题目解答
# include <stdio.h>
#define ll long long
//只需算 i+1->i+k即可
//那么即为 1->i+k 减去 1->i ;
int main()
{
ll i,n,k,ans;
ll x,sum[1010000];
scanf("%lld %lld",&n,&k);
if(k>n-1)//n个城市之间有n-1条路
{
printf("%d",0);
return 0;
}
for(i=1;i<n;i++)
{
scanf("%lld",&x);//相邻两条路之间耗费的距离
sum[i]=sum[i-1]+x;
}
ans=sum[k];
for(i=2;i<=n-k;i++)
ans=fmax(ans,sum[i+k-1]-sum[i-1]);//i>i+k-1
// ans=sum[n-k-1]-sum[0];
printf("%lld",sum[n-1]-ans);
return 0;
}二维前缀和
问题引入
输入一个n行m列的整数矩阵,再输入q个询问,每个询问包含四个整数x1, y1, x2, y2,表示一个子矩阵的左上角坐标和右下角坐标。对于每个询问输出子矩阵中所有数的和。
二维前缀和:
同一维前缀和一样,我们先来定义一个二维数组s[][] , s[i][j] 表示二维数组中,左上角(1, 1)到右下角(i, j)所包围的矩阵元素的和。接下来推导二维前缀和的公式。
算法原理
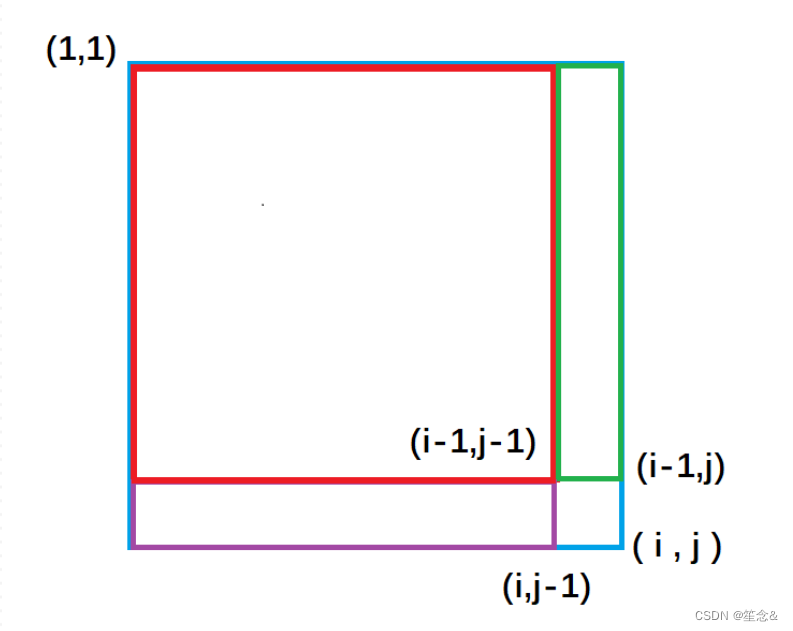
紫色面积是指(1, 1)左上角到(i, j - 1)右下角的矩形面积, 绿色面积是指(1, 1)左上角到(i - 1, j )右下角的矩形面积。每一个颜色的矩形面积都代表了它所包围元素的和。
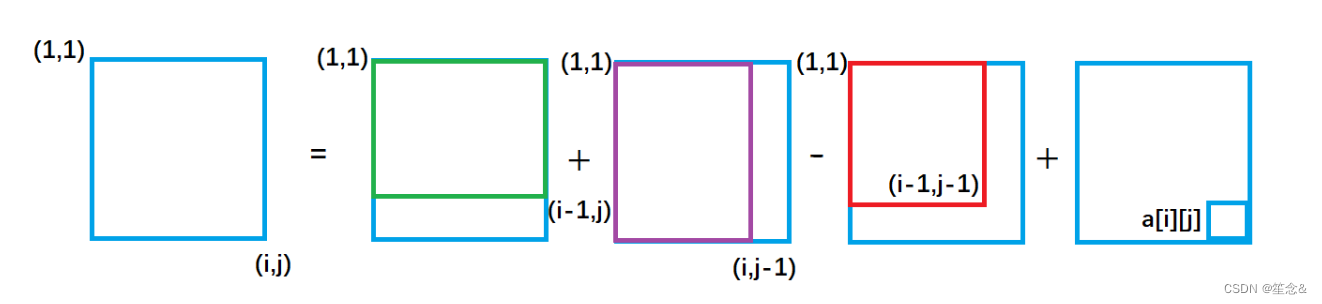
从图中我们很容易看出,整个外围蓝色矩形面积s[i][j] = 绿色面积s[i - 1][j] + 紫色面积s[i][j - 1] - 重复加的红色的面积s[i - 1][j - 1] + 小方块的面积a[i][j];
因此得出二维前缀和预处理公式
s[i][j] = s[i - 1][j] + s[i][j - 1 ] + a[i] [j] - s[i - 1][j - 1]
问题解答
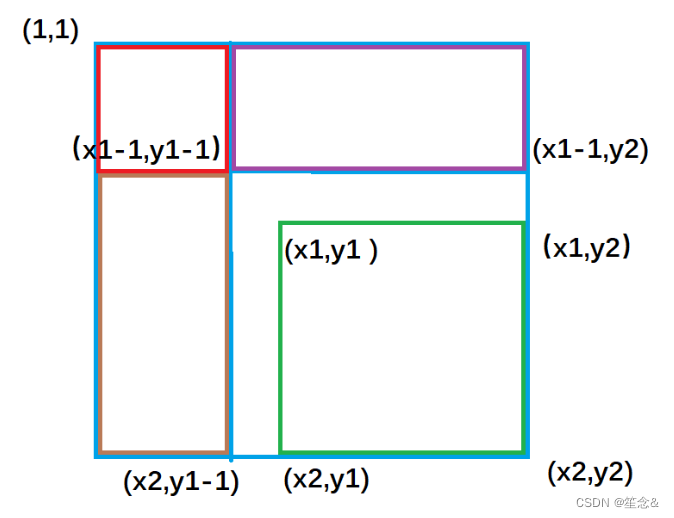
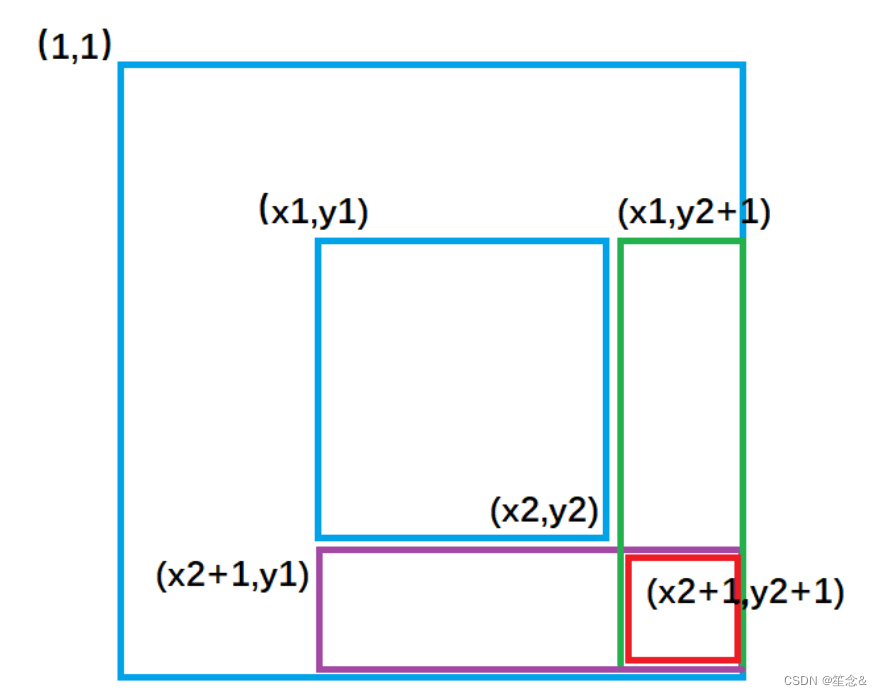
求以(x1,y1)为左上角和以(x2,y2)为右下角的矩阵的元素的和。
紫色面积是指 (1, 1)左上角到(x1 - 1, y2)右下角的矩形面积 ,黄色面积是指(1, 1)左上角到(x2, y1 - 1)右下角的矩形面积;
不难推出:
绿色矩形的面积 = 整个外围面积s[x2, y2] - 黄色面积s[x2, y1 - 1] - 紫色面积s[x1 - 1, y2] + 重复减去的红色面积 s[x1 - 1, y1 - 1]
因此二维前缀和的结论为:
以(x1, y1)为左上角,(x2, y2)为右下角的子矩阵的和为:s[x2, y2] - s[x1 - 1, y2] - s[x2, y1 - 1] + s[x1 - 1, y1 - 1]
#include <iostream>
using namespace std;
const int N = 1010;
int n, m, q;
int s[N][N];
int main()
{
scanf("%d%d%d", &n, &m, &q);
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
scanf("%d", &s[i][j]);
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
while (q -- )
{
int x1, y1, x2, y2;
scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
printf("%d\n", s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]);
}
return 0;
}
二 差分
算法定义
前缀和的一个应用是差分,差分是前缀和的逆运算
定义:
首先给定一个原数组a:a[1], a[2], a[3],,,,,, a[n];
然后我们构造一个数组b : b[1], b[2], b[3],,,,,, b[i];
使得 a[i] = b[1] + b[2] + b[3] + ,,,,,, + b[i]
也就是说,a数组是b数组的前缀和数组,反过来我们把b数组叫做a数组的差分数组。换句话说,
每一个a[i]都是b数组中从头开始的一段区间和。
构造差分数组
a[0 ]= 0;
b[1] = a[1] - a[0];
b[2] = a[2] - a[1];
b[3] = a [3] - a[2];
........
b[n] = a[n] - a[n - 1];
我们只要有b数组,通过前缀和运算,就可以在O(n) 的时间内得到 a 数组 。
算法分类
算法作用
差分是一种处理数据的巧妙而简单的方法,他应用于区间的修改和询问问题。把给定的数据集A分成很多区间,对这些区间做多此操作,每次操作是对某个区间的所有元素做相同的加减操作,若一个格的修改区间内的每个元素,非常耗时。引入差分数组D,当修改某个区间是,只需要修改这个区间的端点,就能记录整个区间的修改,而对端点的修改非常容易,复杂度为O(1)。当所有修改操作结束后,再利用差分数组计算出新的A.复杂度为O(n),m次区间修改和一次查询,总复杂度为O(m+n)
一维差分
问题引入
给定区间[l, r ],让我们把a数组中的[l, r] 区间中的每一个数都加上c,即 a[l] + c , a[l + 1] + c , a[l + 2] + c ,,,,,, a[r] + c;
暴力法:
是for循环l到r区间,时间复杂度O(n),如果我们需要对原数组执行m次这样的操作,时间复杂度就会变成O(n * m)
暴力做法是for循环l到r区间,时间复杂度O(n),如果我们需要对原数组执行m次这样的操作,时间复杂度就会变成O(n * m)
差分法:
算法原理
提示:a数组是b数组的前缀和数组
比如对b数组的b[i]的修改,会影响到a数组中从a[i]及往后的每一个数。
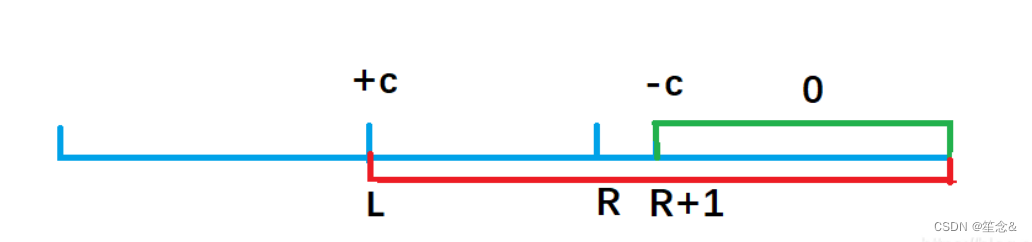
首先让差分b数组中的 b[l] + c ,通过前缀和运算,a数组变成 a[l] + c ,a[l + 1] + c,,,,,, a[n] + c;
然后我们打个补丁,b[r + 1] - c, 通过前缀和运算,a数组变成 a[r + 1] - c,a[r + 2] - c,,,,,,,a[n] - c;
打补丁的理由:
b[l] + c,效果使得a数组中 a[l] 及以后的数都加上了c(红色部分),但我们只要求l到r 区间加上 c, 因此还需要执行 b[r + 1] - c,让a数组中 a[r + 1]及往后的区间再减去c(绿色部分),这样对于a[r] 以后区间的数相当于没有发生改变。
因此我们得出一维差分结论:给a数组中的[ l, r] 区间中的每一个数都加上c,只需对差分数组b做 b[l] + = c, b[r+1] - = c 。时间复杂度为O(1), 大大提高了效率。
问题解答
#include<iostream>
using namespace std;
const int N = 1e5 + 10;
int a[N],b[N];
int main()
{
int n,m;
scanf("%d%d", &n, &m);
for(int i = 1;i <= n; i++)
{
scanf("%d", &a[i]);
b[i] = a[i] - a[i - 1]; //构建差分数组
}
int l, r, c;
while(m--)
{
scanf("%d%d%d", &l, &r, &c);
b[l] += c; //表示将序列中[l, r]之间的每个数加上c
b[r + 1] -= c;
}
for(int i = 1;i <= n; i++)
{
b[i] += b[i - 1]; //求前缀和运算
printf("%d ",b[i]);
}
return 0;
}
算法实践
语文成绩
问题描述
语文考试结束了,成绩还是一如既往地有问题。
小江老师总是写错成绩,所以当她修改成绩的时候,总是累得不行。她总是要一遍遍地给某些同学
增加分数,又要注意最低分是多少。你能帮帮她吗?
输入:
第一行有两个整数n,p,代表学生数与增加分数的次数第二行有n 个数,a1 ~ an,代表各个学生的初始成绩接下来p行,每行有三个数,t,y,z,代表给第 a 个到第 y 个学生每人增加Z 分。
输出:
输出仅一行,代表更改分数后,全班的最低分
样例:
输入
3 2 1 1 1 1 2 1 2 3 1
输出
2
问题解答
# include <stdio.h>
#define ll long long
long long cmp(const void *a,const void *b)
{
return *(int *)a-*(int *)b;
}
int main()
{
ll i,n,p,x,y,z,a[5000001],b[5000001];
scanf("%lld %lld",&n,&p);//学生数和增加分数的次数
for(i=1;i<=n;i++)
{
scanf("%lld",&a[i]);
b[i]=a[i]-a[i-1];//构造差分数组
}
while(p--)
{
scanf("%lld %lld %lld",&x,&y,&z);//x,->y个同学加z分
b[x]+=z;
b[y+1]-=z;
}
for(i=1;i<=n;i++)
b[i]+=b[i-1];//求前缀和
qsort(&b[1],n,sizeof(b[1]),cmp);
printf("%d",b[1]);
return 0;
}小技巧:
上面的求前缀和部分,原本应该写成
a[i]=a[i-1]+b[i];可以省略a,从而节省空间,在后面求原数组a[]时,把已经使用过的较小的b【】直接当作a【】即可,这个技巧在后面的二维差分也可以用到,可以节省一半的空间。
一维差分的局限性
,利用差分数组D[]可以把 O(n)的区间修改变成 O(1)的端点修改
从而提高了修改操作的效率。
但是,一次查询操作,即查询某个 a[],需要用 D[]计算整个原数组 a[],计算量为O(n),即一次查询的复杂
度为 O(n)。在上一例题中,如果查询不是发生了一次,而是有 m次修改,有k 次查询,且修改和查询的
顺序是随机的,此时 m 次修改复杂度为 O(m),k 次查询复杂度为 O(kn),总复杂度为 O(m+kn),还不如
直接用暴力法,总复杂度为 O(mn+k)。
这种题型属于“区间修改+单点查询”,差分数组往往不够用。
因为差分数组对“区间修改很高效,但是对“单点查询”并不高效。此时需要用树状数组和线段树求解
二维差分
问题引入
输入一个n行m列的整数矩阵,再输入q个操作,每个操作包含五个整数x1, y1, x2, y2, c,其中(x1, y1)和(x2, y2)表示一个子矩阵的左上角坐标和右下角坐标。
每个操作都要将选中的子矩阵中的每个元素的值加上c。
请你将进行完所有操作后的矩阵输出。
算法原理
a[][]数组是b[][]数组的前缀和数组,那么b[][]是a[][]的差分数组
原数组: a[i][j]
我们去构造差分数组: b[i][j]
使得a数组中a[i][j]是b数组左上角(1,1)到右下角(i,j)所包围矩形元素的和。
构造二维差分数组
其实关于差分数组,我们并不用考虑其构造方法,因为我们使用差分操作在对原数组进行修改的过程中,实际上就可以构造出差分数组。
同一维差分,我们构造二维差分数组目的是为了 让原二维数组a中所选中子矩阵中的每一个元素加上c的操作,可以由O(n*n)的时间复杂度优化成O(1)
已知原数组a中被选中的子矩阵为 以(x1,y1)为左上角,以(x2,y2)为右下角所围成的矩形区域;
始终要记得,a数组是b数组的前缀和数组,比如对b数组的b[i][j]的修改,会影响到a数组中从a[i][j]及往后的每一个数。
假定我们已经构造好了b数组,类比一维差分,我们执行以下操作
来使被选中的子矩阵中的每个元素的值加上c
b[x1][y1] + = c ;
b[x1,][y2+1] - = c;
b[x2+1][y1] - = c;
b[x2+1][y2+1] + = c;
每次对b数组执行以上操作,等价于
for(int i = x1;i <= x2;i++)
for(int j = y1;j <= y2;j++)
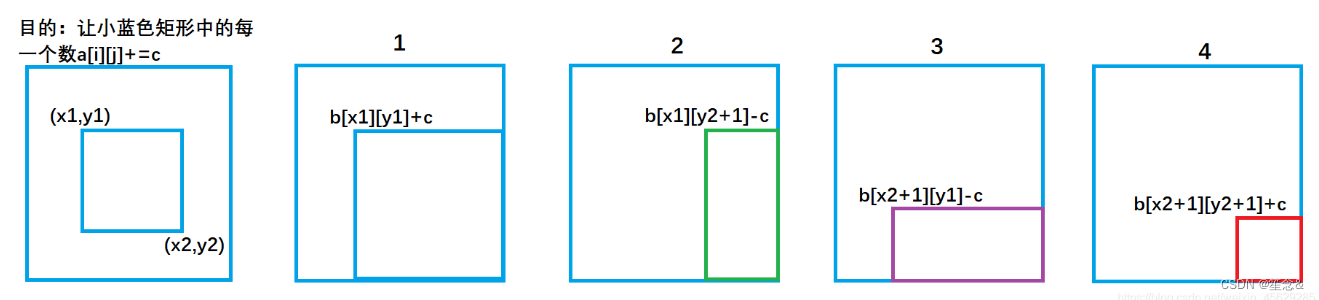
a[i][j] += c;理解过程:
b[x1][y1] += c ; 对应图1 ,让整个a数组中蓝色矩形面积的元素都加上了c。
b[x1,][y2 + 1] -= c ; 对应图2 ,让整个a数组中绿色矩形面积的元素再减去c,使其内元素不发生改变。
b[x2 + 1][y1] -= c ; 对应图3 ,让整个a数组中紫色矩形面积的元素再减去c,使其内元素不发生改变。
b[x2 + 1][y2 + 1] += c; 对应图4,让整个a数组中红色矩形面积的元素再加上c,红色内的相当于被减了两次,再加上一次c,才能使其恢复。
我们将上述操作封装成一个插入函数:
void insert(int x1,int y1,int x2,int y2,int c)
{ //对b数组执行插入操作,等价于对a数组中的(x1,y1)到(x2,y2)之间的元素都加上了c
b[x1][y1] += c;
b[x2 + 1][y1] -= c;
b[x1][y2 + 1] -= c;
b[x2 + 1][y2 + 1] += c;
}
我们可以先假想a数组为空,那么b数组一开始也为空,但是实际上a数组并不为空,因此我们每次
让以(i,j)为左上角到以(i,j)为右下角面积内元素(其实就是一个小方格的面积)去插入 c = a[i][j] ,等价
于原数组a中(i,j) 到(i,j)范围内 加上了 a[i][j] ,因此执行 n*m次插入操作,就成功构建了差分b数组.
代码如下:
for(int i = 1;i <= n;i++)
{
for(int j = 1;j <= m;j++)
{
insert(i, j, i, j, a[i][j]); //构建差分数组
}
}
当然关于二维差分操作也有直接的构造方法,公式如下:
b[i][j] = a[i][j] − a[i − 1][j] − a[i][j − 1] + a[i −1 ][j − 1]
问题解答
#include<iostream>
#include<cstdio>
using namespace std;
const int N = 1e3 + 10;
int a[N][N], b[N][N];
void insert(int x1, int y1, int x2, int y2, int c)
{
b[x1][y1] += c;
b[x2 + 1][y1] -= c;
b[x1][y2 + 1] -= c;
b[x2 + 1][y2 + 1] += c;
}
int main()
{
int n, m, q;
cin >> n >> m >> q;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
cin >> a[i][j];
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
insert(i, j, i, j, a[i][j]); //构建差分数组
}
}
while (q--)
{
int x1, y1, x2, y2, c;
cin >> x1 >> y1 >> x2 >> y2 >> c;
insert(x1, y1, x2, y2, c);
}
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1]; //二维前缀和
}
}
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= m; j++)
{
printf("%d ", b[i][j]);
}
printf("\n");
}
return 0;
}
算法实践
地毯
题目描述
在 n x n 的格子上有 m 个地毯
给出这些地毯的信息,问每个点被多少个地毯覆盖
输入格式:
第一行,两个正整数n,m。意义如题所述
接下来m行,每行两个坐标(x1,y1)和(x2,y2),代表 一块地毯,左上角是(x1,y1),右下角是(x2,y2)
输出格式
输出n 行,每行 n 个正整数
第行第列的正整数表示(,) 这个格子被多少个地毯覆盖
样例:
输入:
5 3 2 2 3 3 3 3 5 5 1 2 1 4
输出:
0 1 1 1 0 0 1 1 0 0 0 1 2 1 1 0 0 1 1 1 0 0 1 1 1
样例解释
题目解答
为了节约空间,可以不定义a[][],而是把用过的D[][]看作a[][]
#include<stdio.h>
int D[5000][5000]; //差分数组
//int a[5000][5000]; //原数组,不定义也行
int main(){
int n,m;
scanf("%d %d",&n,&m);
while(m--){
int x1,y1,x2,y2;
scanf("%d %d %d %d",&x1,&y1,&x2,&y2);
D[x1][y1] += 1; D[x2+1][y1] -= 1;
D[x1][y2+1] -= 1; D[x2+1][y2+1] += 1; //计算差分数组
}
for(int i=1;i<=n;++i){//根据差分数组计算原矩阵的值(想象成求小格子的面积和)
for(int j=1;j<=n;++j){ //把用过的D[][]看成a[][],就不用再定义a[][]了
//a[i][j] = D[i][j] + a[i-1][j] + a[i][j-1] - a[i-1][j-1];
//printf("%d ",a[i][j]); //这两行和下面两行的效果一样
D[i][j] += D[i-1][j] + D[i][j-1] - D[i-1][j-1];
printf("%d ",D[i][j]);
}
printf("\n");//换行
}
return 0;
}
三维差分
我不会!!!想看的自己看,加油
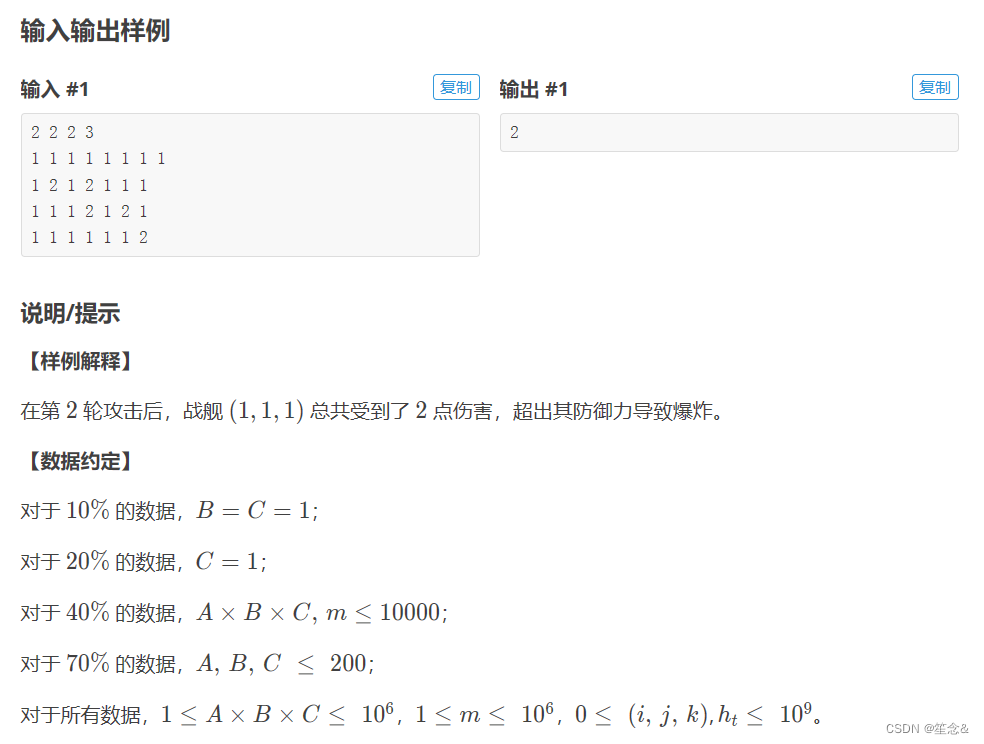
[蓝桥杯 2018 省 A] 三体攻击
代码:
#include<stdio.h>
int A,B,C,n,m;
const int N = 1000005;
int s[N]; //存储舰队生命值
int D[N]; //三维差分数组(压维);同时也用来计算每个点的攻击值
int x2[N], y2[N], z2[N]; //存储区间修改的范围,即攻击的范围
int x1[N], y1[N], z1[N];
int d[N]; //记录伤害,就是区间修改
int num(int x,int y,int z) {
//小技巧:压维,把三维坐标[(x,y,z)转为一维的((x-1)*B+(y-1))*C+(z-1)+1
if (x>A || y>B || z>C) return 0;
return ((x-1)*B+(y-1))*C+(z-1)+1;
}
bool check(int x){ //做x次区间修改。即检查经过x次攻击后是否有战舰爆炸
for (int i=1; i<=n; i++) D[i]=0; //差分数组的初值,本题是0
for (int i=1; i<=x; i++) { //用三维差分数组记录区间修改:有8个区间端点
D[num(x1[i], y1[i], z1[i])] += d[i];
D[num(x2[i]+1,y1[i], z1[i])] -= d[i];
D[num(x1[i], y1[i], z2[i]+1)] -= d[i];
D[num(x2[i]+1,y1[i], z2[i]+1)] += d[i];
D[num(x1[i], y2[i]+1,z1[i])] -= d[i];
D[num(x2[i]+1,y2[i]+1,z1[i])] += d[i];
D[num(x1[i], y2[i]+1,z2[i]+1)] += d[i];
D[num(x2[i]+1,y2[i]+1,z2[i]+1)] -= d[i];
}
//下面从x、y、z三个方向计算前缀和
for (int i=1; i<=A; i++)
for (int j=1; j<=B; j++)
for (int k=1; k<C; k++) //把x、y看成定值,累加z方向
D[num(i,j,k+1)] += D[num(i,j,k)];
for (int i=1; i<=A; i++)
for (int k=1; k<=C; k++)
for (int j=1; j<B; j++) //把x、z看成定值,累加y方向
D[num(i,j+1,k)] += D[num(i,j,k)];
for (int j=1; j<=B; j++)
for (int k=1; k<=C; k++)
for (int i=1; i<A; i++) //把y、z看成定值,累加x方向
D[num(i+1,j,k)] += D[num(i,j,k)];
for (int i=1; i<=n; i++) //最后判断是否攻击值大于生命值
if (D[i]>s[i])
return true;
return false;
}
int main() {
scanf("%d%d%d%d", &A, &B, &C, &m);
n = A*B*C;
for (int i=1; i<=n; i++) scanf("%d", &s[i]); //读生命值
for (int i=1; i<=m; i++) //读每次攻击的范围,用坐标表示
scanf("%d%d%d%d%d%d%d",&x1[i],&x2[i],&y1[i],&y2[i],&z1[i],&z2[i],&d[i]);
int L = 1,R = m; //经典的二分写法
while (L<R) { //对m进行二分,找到临界值。总共只循环了log(m)次
int mid = (L+R)>>1;
if (check(mid)) R = mid;
else L = mid+1;
}
printf("%d\n", R); //打印临界值
return 0;
}