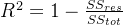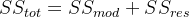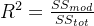python统计分析——一般线性回归模型

Source

参考资料：python统计分析【托马斯】

当我想用一个或多个其他的变量预测一个变量的时候，我们可以用线性回归的方法。

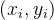
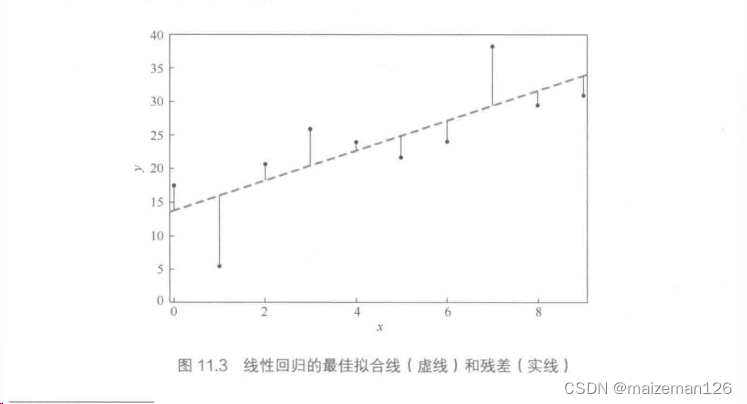
例如，当我们寻找给定数据集 (x_i,y_i) 的最佳拟合线的时候，我们是在寻找让下式的残差平方和最小的参数(k,d)：

$y_i=k\times x_i+d+\varepsilon _i$

其中，k是线的斜率，d是截距。残差是观测值和预测值之间的差异。

由于线性回归方程是用最小化残差平方和的方法来解决的，线性回归又是也成为普通最小二乘法（OLS）回归。

这里注意：与相关性相反，x和y之间的这种关系不再是对称的；它假设x值是精确的，所有的变异性都在于残差。

1、决定系数

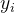
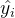
我们约定： y_i 是数据集中的观测值， $\hat{y_i}$ 为模型计算得到的于 y_i 相对应的预测值， $\bar{y}$ 为所有 y_i 的平均值。那么：

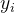
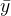
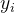
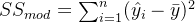
$SS_{mod}=\sum_{i=1}^n(\hat{y_i}-\bar{y})^2$ 是模型平方和，或回归平方和，或可解释平方和。

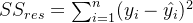
$SS_{res}=\sum_{i=1}^n(y_i-\hat{y_i})^2$ 是残差平方和，或误差平方和。

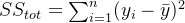
$SS_{tot}=\sum_{i=1}^n(y_i-\bar{y})^2$ 是总平方和，它等于样本方差乘以n-1。

决定系数一般表示为：

$R^2=1-\frac{SS_{res}}{SS_{tot}}$

由于 $SS_{tot}=SS_{mod}+SS_{res}$

所以：

$R^2=\frac{SS_{mod}}{SS_{tot}}$

用文字表达：决定系数就是模型的可解释平方和与总平方和的比值。

对于简单线性回归（即直线拟合），决定系数就是相关系数ｒ的平方。如果我们的自变量和因变量之间存在非线性关系，那么简单的相关性和决定系数会对结果造成误导。

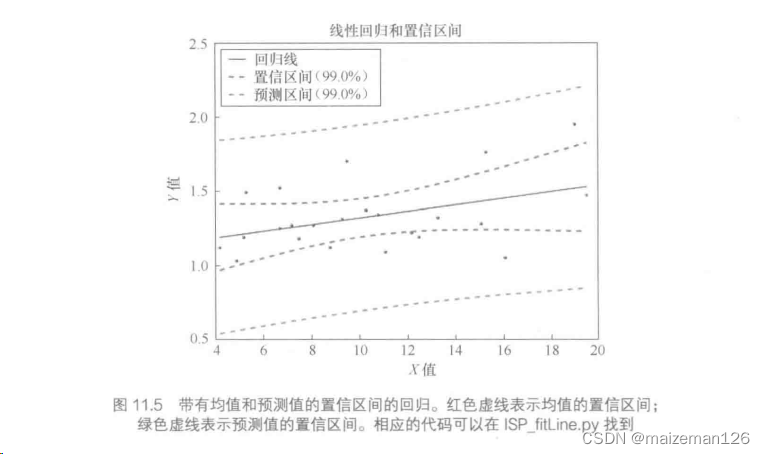
2、带置信区间的直线

对于单变量分布，基于标准差的置信区间表示我们期望包含95%的数据的区间（用于数据）；而基于平均数标准误的置信区间表示95%概率下包含真正均值的区间（用于参数）。如下：

3、曲线拟合

为了了解如何使用不同的模型来评估给定的数据集，让我们来看一个简单的例子：拟合一个有噪声的、略微二次项弯曲的曲线。让我们从numpy中实现的算法开始，然后用线性、二次方、三次方曲线来拟合数据。

代码如下：

# 导入库
import numpy as np
import matplotlib.pyplot as plt

# 生成一个有噪声、略微二次项弯曲的数据集
x=np.arange(100)
y=150+3*x+0.3+x**2+5*np.random.randn(len(x))

# 线性拟合、二次方拟合、三次方拟合
# 创建设计矩阵
M1=np.vstack((np.ones_like(x),x)).T
M2=np.vstack((np.ones_like(x),x,x**2)).T
M3=np.vstack((np.ones_like(x),x,x**2,x**3)).T

# 解方程
p1=np.linalg.lstsq(M1,y)
p2=np.linalg.lstsq(M2,y)
p3=np.linalg.lstsq(M3,y)

np.set_printoptions(precision=3)
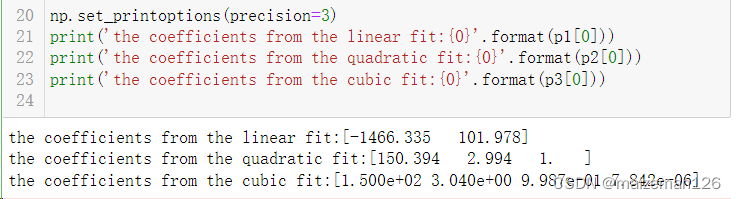
print('the coefficients from the linear fit:{0}'.format(p1[0]))
print('the coefficients from the quadratic fit:{0}'.format(p2[0]))
print('the coefficients from the cubic fit:{0}'.format(p3[0]))

# 计算x对应的预测值
p1_y=-1466.335+101.978*x
p2_y=150.394+2.994*x+x**2
p3_y=150+3.04*x+0.9987*x**2+7.842*(10**(-6))*x**3

# 作图
plt.rcParams['font.sans-serif']="SimHei"    # 设置中文显示
plt.rcParams['axes.unicode_minus']=False    # 设置负号显示
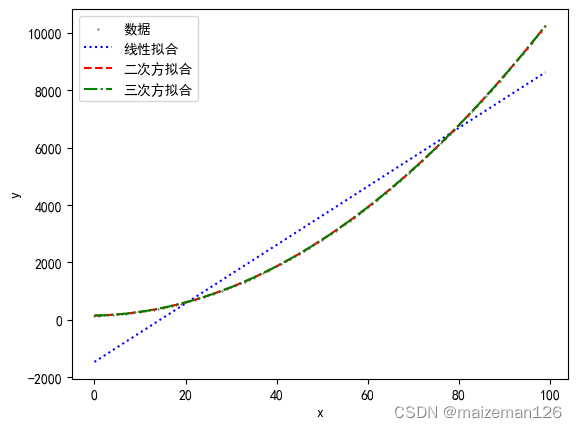
plt.scatter(x,y,c="black",s=0.1,label="数据")
plt.plot(x,p1_y,"b:",label="线性拟合")
plt.plot(x,p2_y,"r--",label="二次方拟合")
plt.plot(x,p3_y,'g-.',label="三次方拟合")
plt.xlabel('x')
plt.ylabel('y')
plt.legend()

显示图片如下

如果我们想找到哪个才是拟合的“最好的”，我们可以使用statsmodels提供的工作来再次拟合模型。使用statsmodels，我们不仅可以得到最佳拟合参数，还能得到关于模型的许多价值的额外信息。python代码如下：

import statsmodels.api as sm
import statsmodels.formula.api as smf

Res1=sm.OLS(y,M1).fit()
Res2=sm.OLS(y,M2).fit()
Res3=sm.OLS(y,M3).fit()

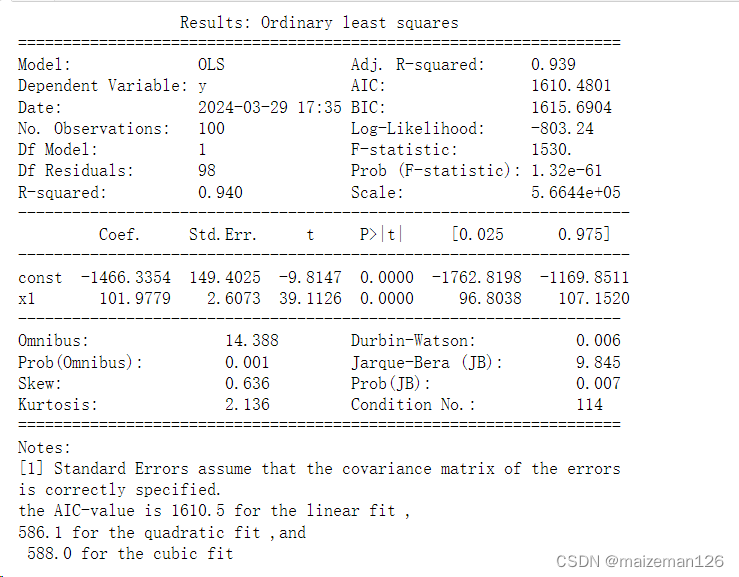
# 以Res1为例输出结果
print(Res1.summary2())
print('the AIC-value is {0:4.1f} for the linear fit ,\n{1:4.1f} for the quadratic fit ,and \n {2:4.1f} for the cubic fit'.format(Res1.aic,Res2.aic,Res3.aic))

在这里，我们需要知道AIC值（Akaike信息准则）可用于评估模型的质量：AIC值越低，模型越好。我们看到，二次模型的AIC值最小，因此是最好的模型：它提供了与三次方模型相同的拟合质量，但使用较少的参数来得到该质量。

下面我们再用公式语言执行相同的拟合，但不需要手动生成设计矩阵，以及如何提取模型参数、标准误和置信区间。值得注意的是，使用pandas数据框允许Python添加单独参数的信息。

import pandas as pd
import statsmodels.formula.api as smf

# 将数据转化为pandas的dataframe格式
df=pd.DataFrame({"x":x,"y":y})

# 拟合模型，并展示结果
Res1F=smf.ols("y~x",df).fit()
Res2F=smf.ols("y~x+I(x**2)",df).fit()
Res3F=smf.ols("y~x+I(x**2)+I(x**3)",df).fit()

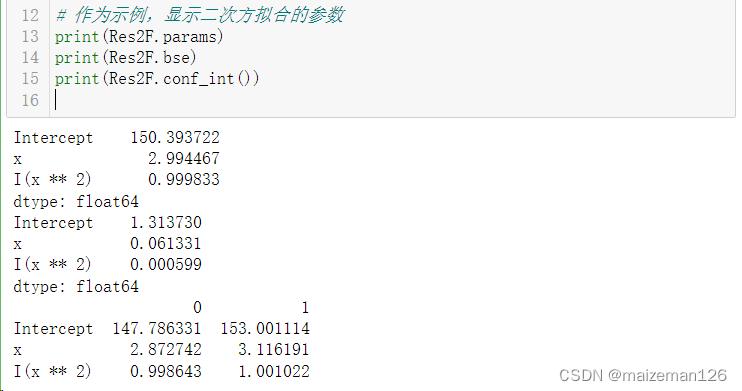
# 作为示例，显示二次方拟合的参数
print(Res2F.params)
print(Res2F.bse)
print(Res2F.conf_int())