char类型用于存储字母和标点符号之类的字符
在技术实现上,char是整数类型,因为char类型实际存储的是整数而不是字符
为了处理字符,计算机使用一种数字编码,用特定的整数表示特定的字符
经典和常用的是ASCII码,标准ADCII码值的范围为0~127
其他字符集:
1)Unicode字符集,能够表示世界范围内多种字符集系统,目前已有超过96000个字符
2)国际标准化组织(ISO)和国际电工技术委员会(IEC)为字符集开发的ISO/IEC 10646标准,Unicode与10646保持兼容
一、char类型变量的声明
char a;
char b, c;二、字符常量及其初始化
char code = 'A';单引号中的一个字符是C的一个字符常量,编译器在编译时会自动将其转换为相应的编码值
char code = 'A'; // 将A视为一个字符常量
char code = A; // 将A视为一个变量名
char code = "A"; // 将A视为一个字符串字符实际上以数值的形式存储,也可以使用数值编码赋值:
char code = 65;这种赋值方式有效的前提是系统采用的是ASCII码,因此实际中推荐使用字符常量赋值,而不是数值编码赋值
三、非打印字符
非打印字符:退格、换行等字符
非打印字符的3种表示方法:
1)使用数值编码赋值
char beep = 7; // 蜂鸣字符的ASCII值为72)使用特殊的符号序列——转义序列(Escape Sequence)
| 序列 | 意义 | 备注 |
| \a | 警报 | 具体现象取决于计算机硬件 |
| \b | 退格 | 常用的输出设备控制字符 不一定适用于所有设备 |
| \f | 走纸 | |
| \n | 换行 | |
| \r | 回车 | |
| \t | 水平制表符 | |
| \v | 垂直制表符 | |
| \\ | 反斜杠(\) | 保证使用\, ', "时不会与指令冲突 |
| \' | 单引号(') | |
| \" | 双引号(") | |
| \? | 问号(?) | |
| \0oo | 八进制(o表示一个八进制数字) |
|
| \xhh | 十六进制(h表示一个十六进制数字) |
3)使用十六进制形式表示字符常量(C90标准开始):反斜杠后跟一个x或X,再加上1到3位十六进制数字
四、字符的打印
printf()函数使用%c说明符打印一个字符
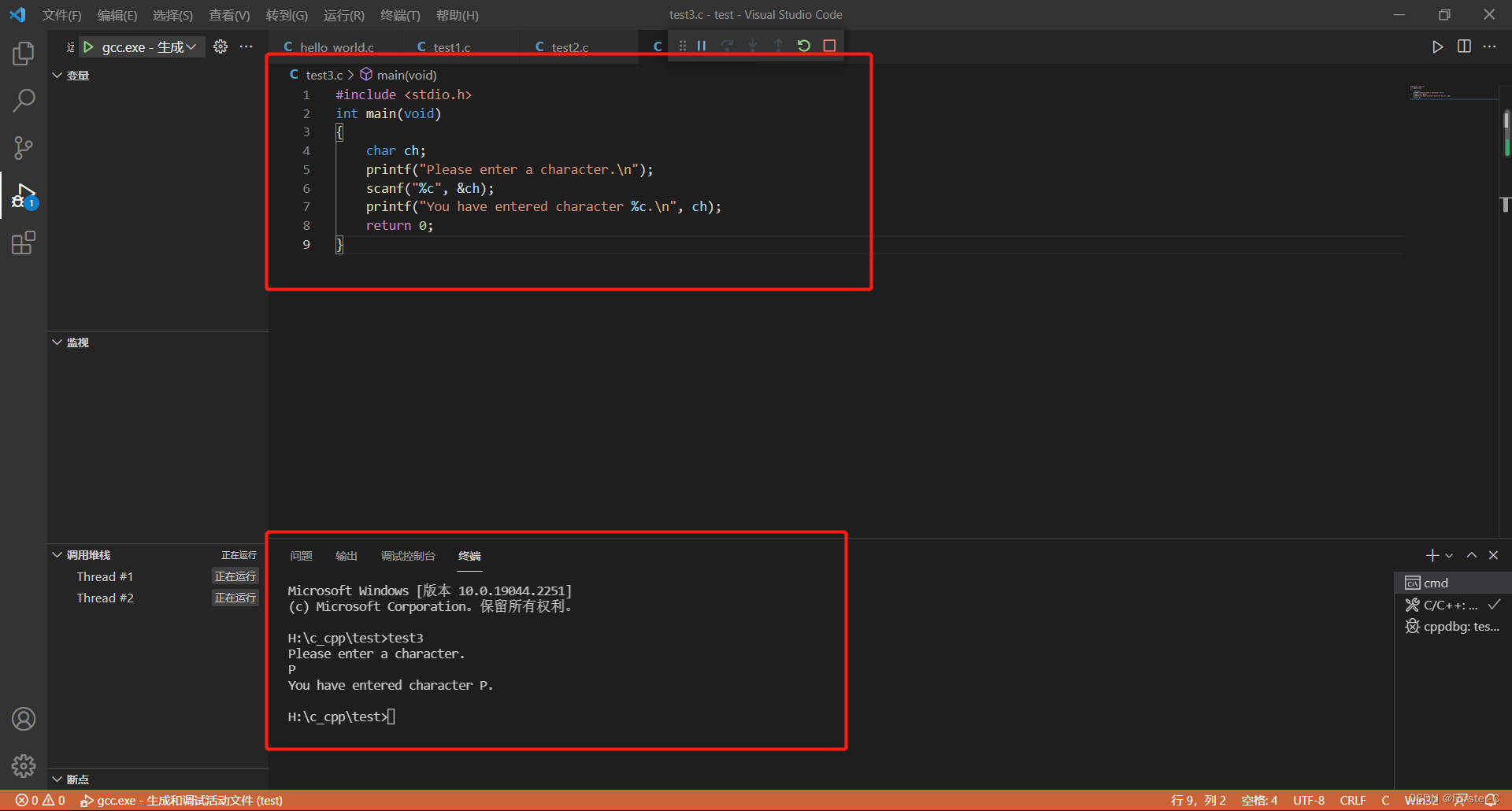
#include <stdio.h>
int main(void)
{
char ch;
printf("Please enter a character.\n");
scanf("%c", &ch);
printf("You have entered character %c.\n", ch);
return 0;
}运行结果:
五、有符号和无符号
一些C实现把char当做有符号类型,其类型值的典型范围为-128~127;一些C实现把char当做无符号类型,其类型值的典型范围为0~255;具体需要查编译器手册,或者通过limits.h头文件查询
在C90标准中,C允许在char之前使用unsigned和signed,无论默认char是有符号或无符号,unsigned char表示无符号,signed char表示有符号;处理小整数时,使用带修饰词的char类型,处理字符时,使用不带修饰词的标准char类型即可