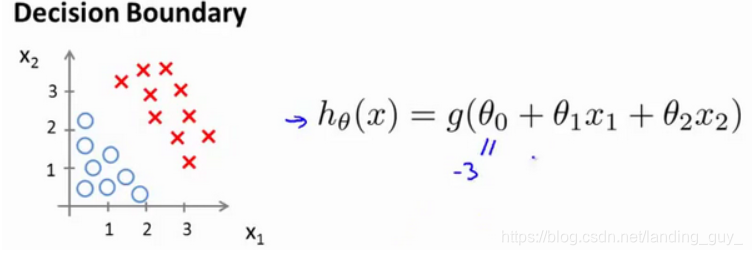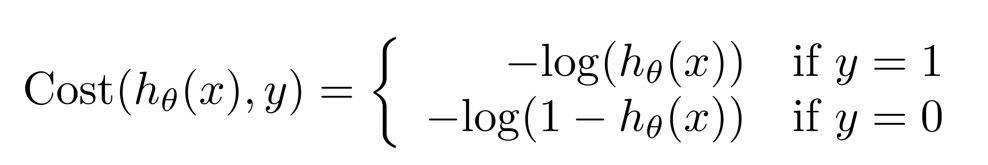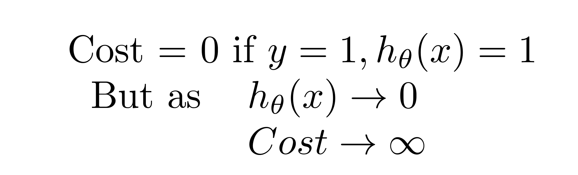前言

• 分类与回归是有监督问题的两个子问题，分类又有二分类与多分类

正文

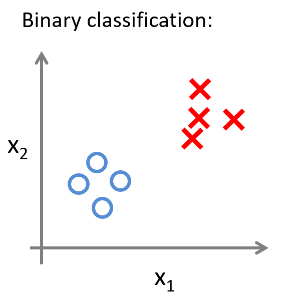
二分类介绍

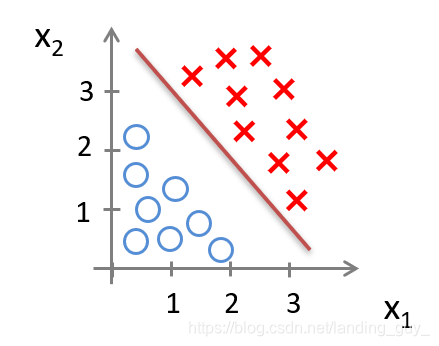
二分类

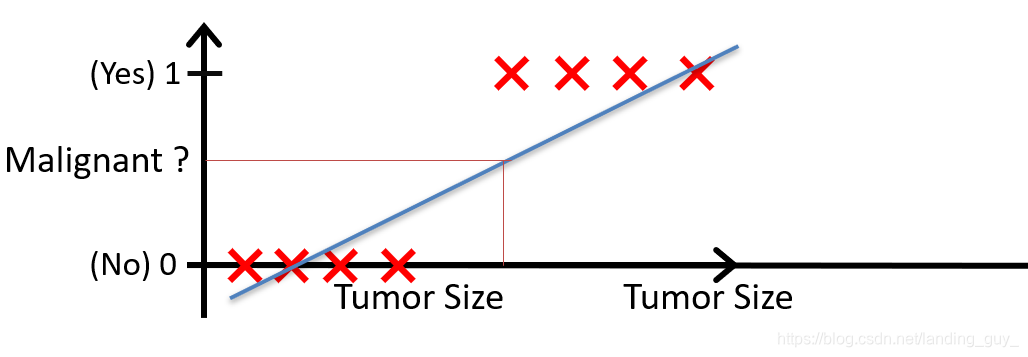
我们可以用线性回归的方法求出适合数据的一条直线：
根据线性回归模型我们只能预测连续的值，然而对于分类问题，我们需要输出0或1，我们可以预测：

当$h_{\theta }\left(x\right)>=0.5$时，预测 $y=1$。

当$h_{\theta }\left(x\right)<0.5$时，预测 $y=0$ 。
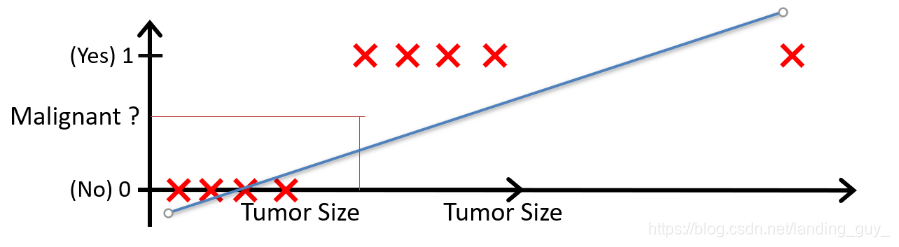
但如果又有一个差距很大的数据，原来的预测就失效了

如果我们要用线性回归算法来解决一个分类问题，对于分类， $y$ 取值为 0 或者1，但如果你使用的是线性回归，那么假设函数的输出值可能远大于 1，或者远小于0，即使所有训练样本的标签 $y$ 都等于 0 或 1。尽管我们知道标签应该取值0 或者1，但是如果算法得到的值远大于1或者远小于0的话，就会感觉很奇怪。所以我们在接下来的要研究的算法就叫做逻辑回归算法，这个算法的性质是：它的输出值永远在0到 1 之间。

逻辑回归模型的假设是： $h_{\theta }\left(x\right)=g\left({\theta }^{T}X\right)$
其中：
$X$ 代表特征向量
$g$ 代表逻辑函数（logistic function)是一个常用的逻辑函数为S形函数（Sigmoid function），公式为： $g\left(z\right)=\frac{1}{1+e^{-z}}$。

• python 代码

def sigmoid(z):
	return 1/(1+np.exp(-z))

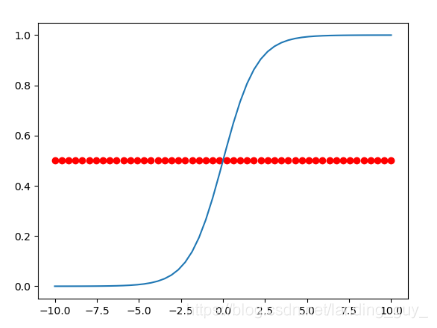
• 图像
  

对模型的理解： $g\left(z\right)=\frac{1}{1+e^{-z}}$。

$h_{\theta }\left(x\right)$的作用是，对于给定的输入变量，根据选择的参数计算输出变量=1的可能性（estimated probablity）即$h_{\theta }\left(x\right)=P\left(y=1|x;\theta \right)$
例如，如果对于给定的$x$，通过已经确定的参数计算得出$h_{\theta }\left(x\right)=0.7$，则表示有70%的几率$y$为正向类，相应地$y$为负向类的几率为1-0.7=0.3。

判定边界

现在假设我们有一个模型：

并且参数$\theta$ 是向量[-3 1 1]。 则当$-3+x_1+x_2\ge 0$，即$x_1+x_2\ge 3$时，模型将预测 $y=1$。
我们可以绘制直线$x_1+x_2=3$，这条线便是我们模型的分界线，将预测为1的区域和预测为 0的区域分隔开。

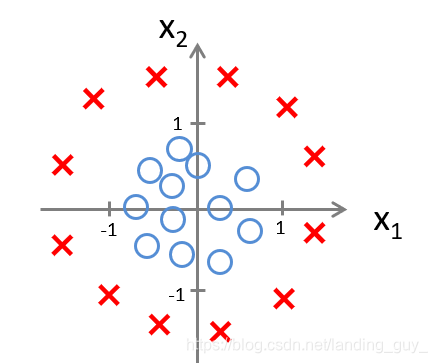
假如我们的数据是这样的分布：

因为需要用曲线才能分隔 $y=0$ 的区域和 $y=1$ 的区域，我们需要二次方特征：$h_{\theta }\left(x\right)=g\left({\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+{\theta }_3{x}_1^2+{\theta }_4{x}_2^2\right)$是[-1 0 0 1 1]，则我们得到的判定边界恰好是圆点在原点且半径为1的圆形。

我们可以用非常复杂的模型来适应非常复杂形状的判定边界。其实这就是深度学习层的堆叠。

二分类中的cost function

线性回归的代价函数为：$J\left(\theta \right)=\frac{1}{m}\sum _{i=1}^m\frac{1}{2}{\left(h_{\theta }\left(x^{\left(i\right)}\right)-y^{\left(i\right)}\right)}^2$ 。
我们重新定义逻辑回归的代价函数为：$J\left(\theta \right)=\frac{1}{m}\sum _{i=1}^{m}Cost\left(h_{\theta }\left(x^{\left(i\right)}\right),y^{\left(i\right)}\right)$，其中

• 这个代价函数比较容易理解，如果标签是正类，就是$-log(h_{\theta }(x))$, 标签是负类也就是0，则为$-log(1-h_{\theta }(x))$， 因为负类的预测概率就是$1-h_{\theta }(x)$嘛。也就是根据正负类加了个-log而已

将构建的 $Cost\left(h_{\theta }\left(x\right),y\right)$简化如下：

$Cost\left(h_{\theta }\left(x\right),y\right)=-y\times log\left(h_{\theta }\left(x\right)\right)-(1-y)\times log\left(1-h_{\theta }\left(x\right)\right)$

代入代价函数得到：

$J\left(\theta \right)=\frac{1}{m}\sum _{i=1}^m[-y^{(i)}\log \left(h_{\theta }\left(x^{(i)}\right)\right)-\left(1-y^{(i)}\right)\log \left(1-h_{\theta }\left(x^{(i)}\right)\right)]$
即：$J\left(\theta \right)=-\frac{1}{m}\sum _{i=1}^m[y^{(i)}\log \left(h_{\theta }\left(x^{(i)}\right)\right)+\left(1-y^{(i)}\right)\log \left(1-h_{\theta }\left(x^{(i)}\right)\right)]$

• Python代码实现：

import numpy as np
    
def cost(theta, X, y):
    
  theta = np.matrix(theta)
  X = np.matrix(X)
  y = np.matrix(y)
  first = np.multiply(-y, np.log(sigmoid(X* theta.T))) #　这是对应位置一一相乘，不是矩阵乘法
  second = np.multiply((1 - y), np.log(1 - sigmoid(X* theta.T)))
  return np.sum(first - second) / (len(X))

在得到这样一个代价函数以后，我们便可以用梯度下降算法来求得能使代价函数最小的参数了。算法为：

Repeat {
${\theta }_j:={\theta }_j-\alpha \frac{\partial }{\partial {\theta }_j}J(\theta )$
(simultaneously update all )
}

求导后得到：

Repeat {
${\theta }_j:={\theta }_j-\alpha \frac{1}{m}\sum _{i=1}^m\left(h_{\theta }\left(x^{\left(i\right)}\right)-y^{\left(i\right)}\right)x_j^{(i)}$
(simultaneously update all )
}

发现和线性回归的损失函数也就是square loss 对应的求导结果是一样的

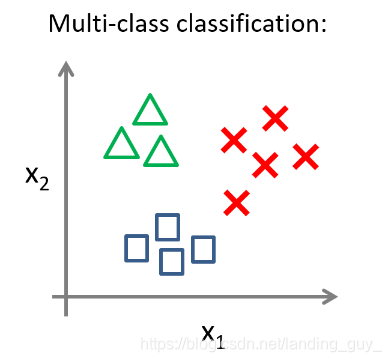
多分类介绍

多分类

对于之前的二元分类问题，我们的数据看起来可能是像这样

对于一个多类分类问题，我们的数据集或许看起来像这样：

一对多算法

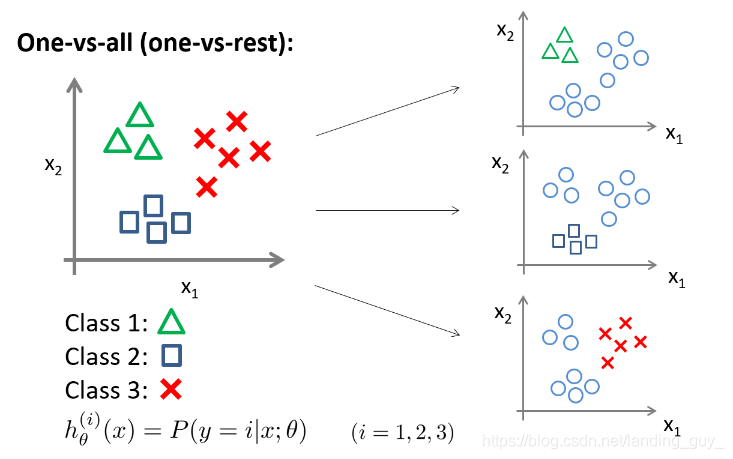
• 在解决多分类的问题时我们先使用一对多(one vs all)算法，具体如下：

• 对于一个数据集，像这样：
  

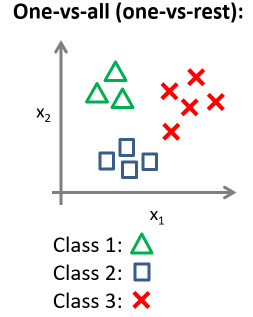
• 用3种不同的符号来代表3个类别，问题就是给出3个类型的数据集，我们如何得到一个学习算法来进行分类呢？

• 可以用三角形表示 $y=1$，方框表示$y=2$，叉叉表示 $y=3$。然后使用一个训练集，将其分成3个二元分类问题。

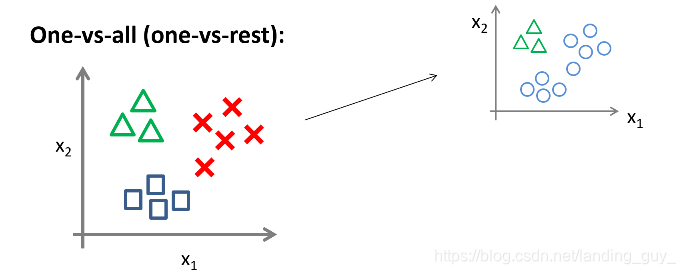
1. 先从用三角形代表的类别1开始，实际上我们可以创建一个，新的"伪"训练集，类型2和类型3定为负类，类型1设定为正类，我们创建一个新的训练集，如下图所示的那样，我们要拟合出一个合适的分类器

这里的三角形是正样本，而圆形代表负样本。可以这样想，设置三角形的值为1，圆形的值为0，下面我们来训练一个标准的逻辑回归分类器，这样我们就得到一个正边界。

2. 为了能实现这样的转变，我们将多个类中的一个类标记为正向类（$y=1$），然后将其他所有类都标记为负向类，这个模型记作$h_{\theta }^{\left(1\right)}\left(x\right)$。接着，类似地我们选择另一个类标记为正向类（$y=2$），再将其它类都标记为负向类，将这个模型记作 $h_{\theta }^{\left(2\right)}\left(x\right)$,依此类推。
最后我们得到一系列的模型简记为： $h_{\theta }^{\left(i\right)}\left(x\right)=p\left(y=i|x;\theta \right)$其中：$i=\left(1,2,3....k\right)$， 如图所示：

3. 最后，在我们需要做预测时，我们将所有的分类机都运行一遍，然后对每一个输入变量，都选择最高可能性的输出变量。

4. 现在要做的就是训练这个逻辑回归分类器：$h_{\theta }^{\left(i\right)}\left(x\right)$， 其中 $i$ 对应每一个可能的 $y=i$，最后，为了做出预测，我们给出输入一个新的 $x$ 值，用这个做预测。我们要做的就是在我们三个分类器里面输入 $x$，然后我们选择一个让 $h_{\theta }^{\left(i\right)}\left(x\right)$ 最大的$i$，即$\underset{i}{\max }{h}_{\theta }^{\left(i\right)}\left(x\right)$。

附录

逻辑回归推导过程

推导过程：

$J\left(\theta \right)=-\frac{1}{m}\sum _{i=1}^m[y^{(i)}\log \left(h_{\theta }\left(x^{(i)}\right)\right)+\left(1-y^{(i)}\right)\log \left(1-h_{\theta }\left(x^{(i)}\right)\right)]$
考虑：
$h_{\theta }\left(x^{(i)}\right)=\frac{1}{1+e^{-{\theta }^T{x}^{(i)}}}$
则：
$y^{(i)}\log \left(h_{\theta }\left(x^{(i)}\right)\right)+\left(1-y^{(i)}\right)\log \left(1-h_{\theta }\left(x^{(i)}\right)\right)$

$=y^{(i)}\log \left(\frac{1}{1+e^{-{\theta }^T{x}^{(i)}}}\right)+\left(1-y^{(i)}\right)\log \left(1-\frac{1}{1+e^{-{\theta }^T{x}^{(i)}}}\right)$

$=-y^{(i)}\log \left(1+e^{-{\theta }^T{x}^{(i)}}\right)-\left(1-y^{(i)}\right)\log \left(1+e^{{\theta }^T{x}^{(i)}}\right)$

所以：
$\frac{\partial }{\partial {\theta }_j}J\left(\theta \right)=\frac{\partial }{\partial {\theta }_j}[-\frac{1}{m}\sum _{i=1}^m[-y^{(i)}\log \left(1+e^{-{\theta }^T{x}^{(i)}}\right)-\left(1-y^{(i)}\right)\log \left(1+e^{{\theta }^T{x}^{(i)}}\right)]]$

$=-\frac{1}{m}\sum _{i=1}^m[-y^{(i)}\frac{-x_j^{(i)}{e}^{-{\theta }^T{x}^{(i)}}}{1+e^{-{\theta }^T{x}^{(i)}}}-\left(1-y^{(i)}\right)\frac{x_j^{(i)}{e}^{{\theta }^T{x}^{(i)}}}{1+e^{{\theta }^T{x}^{(i)}}}]$

$=-\frac{1}{m}\sum _{i=1}^m{y}^{(i)}\frac{x_j^{(i)}}{1+e^{{\theta }^T{x}^{(i)}}}-\left(1-y^{(i)}\right)\frac{x_j^{(i)}{e}^{{\theta }^T{x}^{(i)}}}{1+e^{{\theta }^T{x}^{(i)}}}]$

$=-\frac{1}{m}\sum _{i=1}^m\frac{y^{(i)}{x}_j^{(i)}-x_j^{(i)}{e}^{{\theta }^T{x}^{(i)}}+y^{(i)}{x}_j^{(i)}{e}^{{\theta }^T{x}^{(i)}}}{1+e^{{\theta }^T{x}^{(i)}}}$

$=-\frac{1}{m}\sum _{i=1}^m\frac{y^{(i)}\left(1\text{+}{e}^{{\theta }^T{x}^{(i)}}\right)-e^{{\theta }^T{x}^{(i)}}}{1+e^{{\theta }^T{x}^{(i)}}}{x}_j^{(i)}$

$=-\frac{1}{m}\sum _{i=1}^m(y^{(i)}-\frac{e^{{\theta }^T{x}^{(i)}}}{1+e^{{\theta }^T{x}^{(i)}}})x_j^{(i)}$

$=-\frac{1}{m}\sum _{i=1}^m(y^{(i)}-\frac{1}{1+e^{-{\theta }^T{x}^{(i)}}})x_j^{(i)}$

$=-\frac{1}{m}\sum _{i=1}^m[y^{(i)}-h_{\theta }\left(x^{(i)}\right)]x_j^{(i)}$

$=\frac{1}{m}\sum _{i=1}^m[h_{\theta }\left(x^{(i)}\right)-y^{(i)}]x_j^{(i)}$

注：虽然得到的梯度下降算法表面上看上去与线性回归的梯度下降算法一样，但是这里的$h_{\theta }\left(x\right)=g\left({\theta }^{T}X\right)$与线性回归中不同，所以实际上是不一样的。另外，在运行梯度下降算法之前，进行特征缩放依旧是非常必要的。

题目及例程

题目一

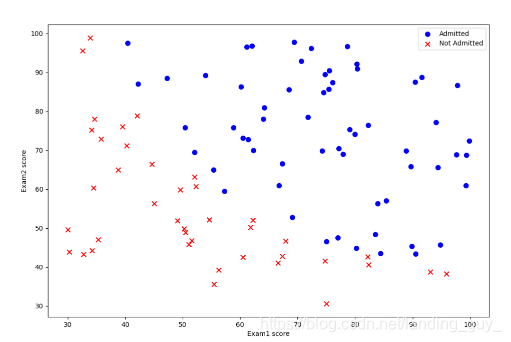
• 假设有学生两次考试的成绩以及考生录取情况的数据，据此做预测其余学生被录取的概率。
• 数据如图：
  
• 绘制数据图像

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd


path = 'ex2data1.txt'
data = pd.read_csv(path, header=None, names=['Exam1', 'Exam2', 'Admitted'])


positive = data[data['Admitted'].isin([1])]
negative = data[data['Admitted'].isin([0])]
# 这里的.isin()是一个用布尔条件的列值来过滤数据的方法， 意为取对应的某一列位置符合条件的所有行
# data['Admitted'].isin([1])就是Admitted这列为1的返回值，为1则为True，反之为False，
# 然后data[data['Admitted'].isin([1])]会把为True地方的所有行取出

fig, ax = plt.subplots(figsize=(12, 8))
# 关于fig，ax的解释参照链接：https://zhuanlan.zhihu.com/p/93423829

ax.scatter(positive['Exam1'], positive['Exam2'], s=50, c='b', marker='o', label='Admitted')
ax.scatter(negative['Exam1'], negative['Exam2'], s=50, c='r', marker='x', label='Not Admitted')
ax.legend()
ax.set_xlabel('Exam1 score')
ax.set_ylabel('Exam2 score')
plt.show()

• 梯度下降

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd


path = 'ex2data1.txt'
data = pd.read_csv(path, header=None, names=['Exam1', 'Exam2', 'Admitted'])



# 数据准备
data.insert(0, 'ones', 1)
X = np.matrix(data.iloc[:, 0:3], dtype='float64')
Y = np.matrix(data.iloc[:, 3:4], dtype='float64')
theta = np.matrix(np.zeros((1, 3)))
alpha = 0.01
iters = 2

def sigmoid(X):
    return 1/(1+np.exp(-X))

def Costfunction(X, Y, theta):
    hx = sigmoid(X*theta.T)
    first = np.multiply(Y, np.log(hx))
    second = np.multiply((1-Y), np.log(1-hx))
    return -1/len(X)*np.sum(first+second)

def GradientDescent(X, Y, theta, alpha, iters):
    cost = []
    temp = np.matrix(np.zeros(3))
    for i in range(iters):
        inner = sigmoid(X*theta.T) - Y
        for j in range(theta.size):
            temp[0,j] = theta[0,j] - alpha/len(X)*np.sum(np.multiply(inner, X[:,j]))
        theta = temp

        cost.append(Costfunction(X, Y, theta))
    return theta, cost

theta, cost = GradientDescent(X, Y, theta, alpha, iters)

注意这里的iters只用了2， 因为在工程上python的sigmoid(38)会直接等于1，无法log。可以使用特征缩放解决，但是pytorch框架下的torch数据类型应该可以。