一、前言
最近AI绘画、聊天、代码生成可以说是刮起了一阵风,席卷了互联网。各大网站都在疯狂刷屏相关的内容,也收到了各界的热烈的关注。无论是AI绘画还是聊天这类的技术都属于同一个领域:人工智能生成内容(AIGC)
小伙伴可能会疑惑,什么是AIGC?
AIGC 即 AI Generated Content,是一种通过人工智能技术来自动或辅助生成内容的内容生成方式,是继专业生产内容(PGC, Professional-generated Content)、用户生产内容(UGC, User-generated Content)之后的新型内容创作方式,具有高效性和自动化的特点。随着深度学习模型不断完善、开源模式的推动,加快了 AIGC 走向落地应用的速度。正如我们所看到的,今年是AIGC爆火的一年,其实在年初并没有多少AIGC相关的内容出现在互联网,但就在这几个月间,迭代和传播速度呈指数级爆发。而且通过其创作的作品有的还能达到专业的级别,甚至“以假乱真”,这给我们带来了惊喜但也带来了忧虑。害怕被AI取代。
人类是否被AI取代的话题也是老生常谈的了,不可否认随着AI的出现和更新一定会带走一些传统的东西,这是无可争议的事实。但我们在面对新的技术变革时,与其担心哪天会被机器替代,不如而思考如何让机器为我们做事,让其成为我们的助手从而更高效,更有价值的完成工作或创造“世界”。所以抱有与技术共生的理念才能拥抱未来的变化。
参与AIGC领域研发的公司有很多,谷歌、Meta、英伟达等巨头都陆续加入了该赛道。但在国内没有几家公司参与其中,主要是因为接口开放的限制,AI生成相关应用难以使用。另一方面模型训练成本是巨大的,这也让不少企业望而却步。
但在我探索的过程中发现一款由昆仑万维集团与合作伙伴奇点智源推出的全系列AIGC模型与算法—“昆仑天工”,可以说是国内独树一帜存在,也在业界处于领先的地位。它们在AI生成能力覆盖图像、音乐、编程、文本等全模态领域都有着杰出的表现。这里将通过该公司的模型和产品深入介绍AIGC在几大方面的应用。
二、生成图像模型
2018年,一幅由 AI 生成的艺术品《埃德蒙·贝拉米肖像》以大约300万人民币的高价成功拍卖,从那时起,AI 艺术生成已经逐步走进大众的视野:
今年出现了大量的文本生成图像模型,尤其是随着Stable Diffusion 的出现,让AI生成图像技术层面带来了质的突破,甚至已经可以生成能够媲美专业画师的作品,生成图片的效率也大大缩短,由原来的数小时到几分钟,甚至一秒就能出图。AI作画能在近期爆火,取得如此巨大进展的原因有很大一部分功劳要归属于它。
Stable diffusion是一个基于Latent Diffusion Models(潜在扩散模型,LDMs)的文图生成(text-to-image)模型
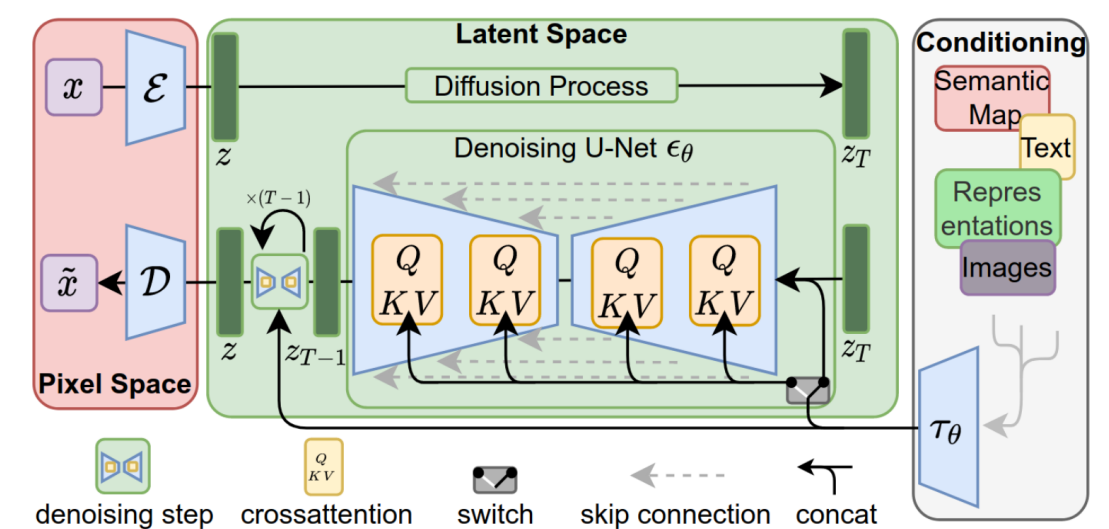
Latent Diffusion Models通过在一个潜在表示空间中迭代“去噪”数据来生成图像,然后将表示结果解码为完整的图像,让文图生成能够在消费级GPU上,在10秒级别时间生成图片,大大降低了落地门槛。
Latent Diffusion Models整体框架如下图,首先需要训练好一个自编码模型(AutoEncoder,包括一个编码器 E 和一个解码器 D )。这样一来,我们就可以利用编码器对图片进行压缩,然后在潜在表示空间上做diffusion操作,最后我们再用解码器恢复到原始像素空间即可:
但是Stable Diffusion 模型并不能通过中文提示词输入来生成相应的图像。值得庆幸的是昆仑天工有一款名为天工巧绘 SkyPaint的AI绘画模型在 Stable Diffusion的基础上做了中文的支持,它也是第一款多语言Stable Diffusion分支模型。
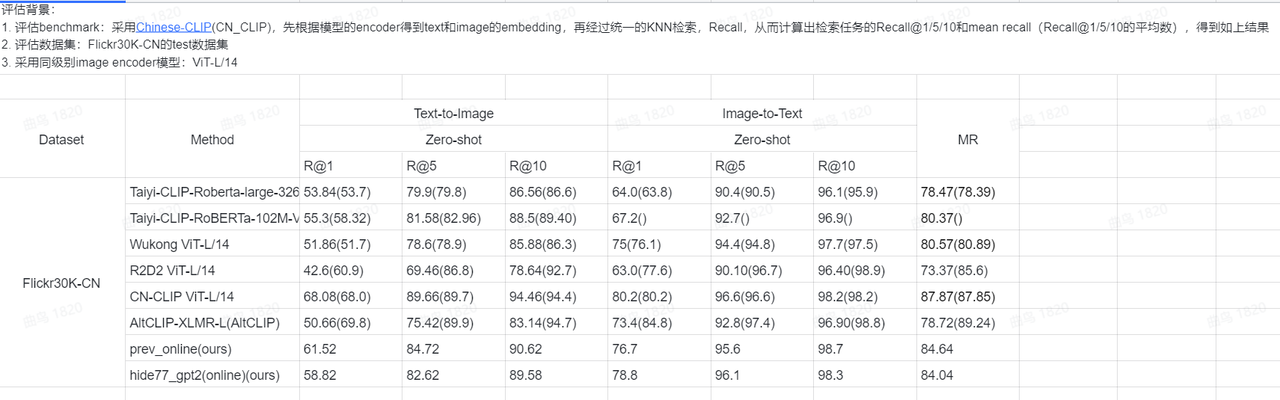
除此之外 SkyPaint 使用 1.5 亿级的平行语料优化提示词模型实现中英文对照,不仅涉及翻译任务语料,还包括了 用户使用频率高的提示词中英语料,古诗词中英语料,字幕语料,百科语料,图片文字描述语料等多场景 多任务的海量语料集合,对模型进行了深度优化,得以让中文文本能够有更好的图像生成效果。 昆仑天工的天工巧绘 SkyPaint 模型均与 当前AI 作画领域最为领先的模型相当,下表对比了不同模型在 Flickr30K-CN 数据集上的性能表现:
在未来,它们还会支持更多语言的提示词输入,更强大的语言生成模型指导图像生成, 风格更加多样,增加更多艺术风格的支持 以及支持用户对生成的图像进行二次提示词编辑图像功能 。
SkyPaint已经发布了微信小程序的体验版本,我也体验了一些,效果确实不错:
输入文本:
生成效果:
三、文本生成模型
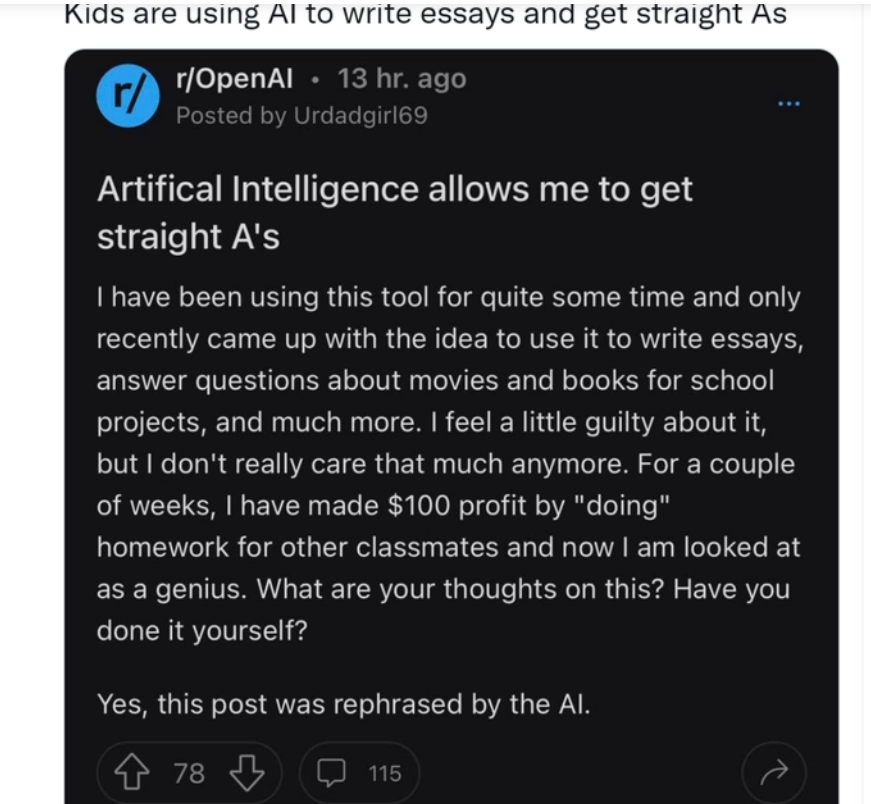
自从人工智能研究公司OpenAI发布其语言模型GPT-3以来,越来越多的学生开始利用AI进行写作。甚至将作业要求输入OpenAI以及类似的程序,这些程序使用深度学习来生成文本能够达到“以假乱真”的效果。比如,一位在Reddit上名叫innovate_rye的生物化学学科的一年级学生,教授会安排一些包括扩展回答的简单家庭作业,当他把“写出生物技术的五件好事和坏事”提交给AI后,系统能给出一个最后评分为A的答案:
上面提到的GPT-3模式是有史以来最大的神经网络,由OpenAI在2020年5月发表的论文“Language Models Are Three Shot Leaners”中首次公开。它具有1750亿个参数,当时震惊了业界。tian
如今也有越来越多基于GPT-3模型的产品出现,最让我印象深刻的还是昆仑万维与奇点智源联合推出的瑶光和天枢模型。
瑶光的性能更强,适用于需要生成大量内容(论文、小说等)场景的应用,天枢则适用于需要实时生成的场景,例如:聊天对话、智能客服等。
它们都拥有多样的下游能力,包括续写,对话,中英翻译,内容风格生成,推理,诗词对联等:
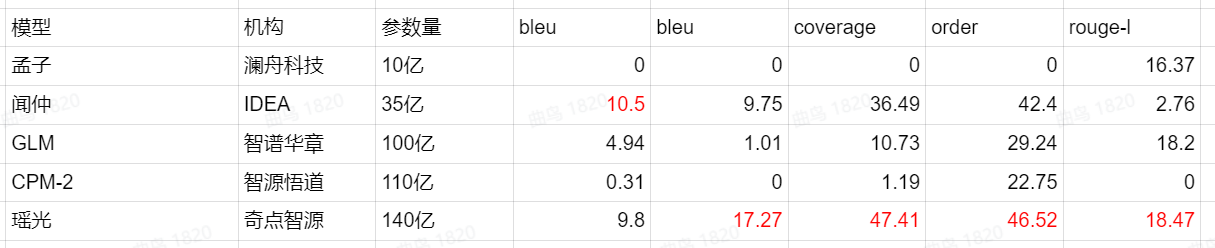
并在各项专业性领域的任务中(例如分类,匹配,填空,识别,识别)表现突出,与现有大模型的比试中也排列前茅(下图是它的“瑶光”模型与市面上主流的其它AI模型的参数对比):
能取得如此优异的成绩得益于他们针对中文领域构建了千亿级别的高质量数据集,通过高性能a100-gpu集群,训练(200张显卡,训练了4周,后续优化合计2周)得到百亿参数量的GPT-3生成模型。
上面提到的对话,中英翻译、对联等功能我们可以在奇点智源官网上体验到。
这里我分享下我体验到的一些功能:
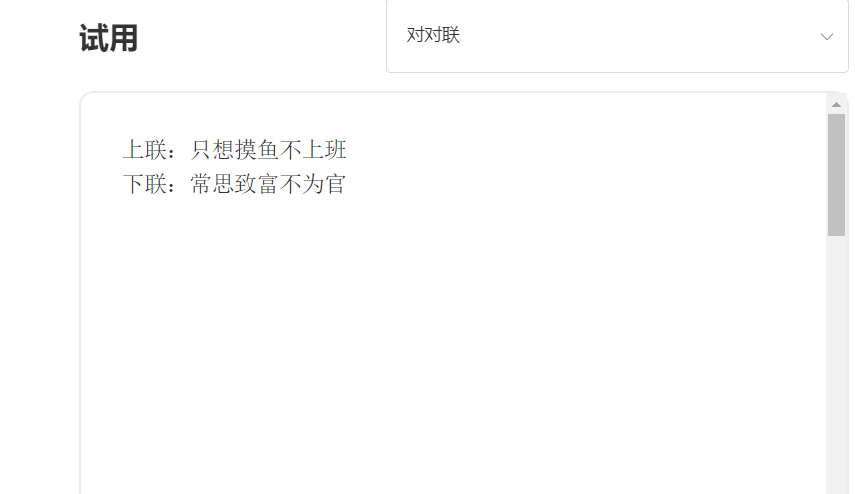
1) 对对联
上联:只想摸鱼不上班,AI生成的下联是:常思致富不为官:
这对出来的:常思致富不为官,确实把我惊艳到了,对的非常工整,也契合上联的含义:。
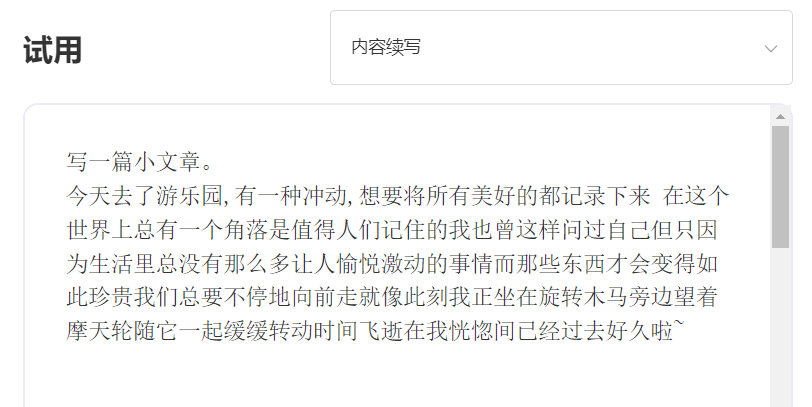
2) 内容续写
我填写的内容是:写一篇小文章。今天去了游乐园
AI生成的内容如下:
也没有偏离题意,而且生成的内容文笔也不错,我们再稍微改改就可以得到一篇佳作了。要是我上学的年代有这样的技术,我的作文分数就不会那么低了。
四、AI生成代码
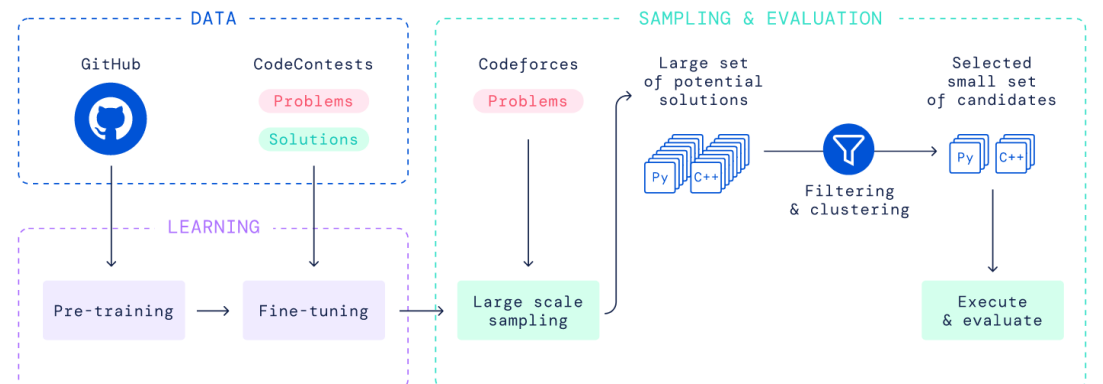
代码自动生成对很多程序员包括我认为都是很难有达到商业级水准的效果,是一项非常复杂、困难的挑战。但随着开发阿尔法go的公司deepmind推出的alphacode让这件事变得不再困难。令人惊讶的是,AlphaCode此前参加了网站Codeforces举行的10场编程比赛,排名前54.3%,击败了46%的参赛者,Elo评分1238。当然现阶段AlphaCode也只不过是在程序员的竞争中混了个一般水平,但随着时间的推移,在它经历越来越多的训练和改进后一定会产生出非常不错的效果。alphacode的原理架构图并不复杂:
-
pretrain:在github的数据集上做pretrain。模型就是BERT,pretrain方法也差不多。
-
fine-tune:在 codeforce 数据集上做 fine-tune,这个模型是标准的基于 transformer 的 encoder-decoder 结构,encoder输入是题目的描述(也包括:题目的tags、solution使用的语言、题目中的样例),decoder的输出对应的ground-truth是一个solution,可以是对的,也可以是错的。
-
用训练完的模型 sample 大量的 solution 出来,并且做过滤和聚类。过滤是为了去掉无法通过样例的代码(会干掉绝大部分),聚类是为了让实现不同但输出相同的代码只提交一次(节约提交的budget)。聚类中,还需要一个独立训练的生成测试数据的模型。这个步骤是针对竞赛题设计的,从这个步骤看,直接用生成的代码直接run错误的概率很高。
-
从聚类最大的类开始挑选,选出10个solution来提交。
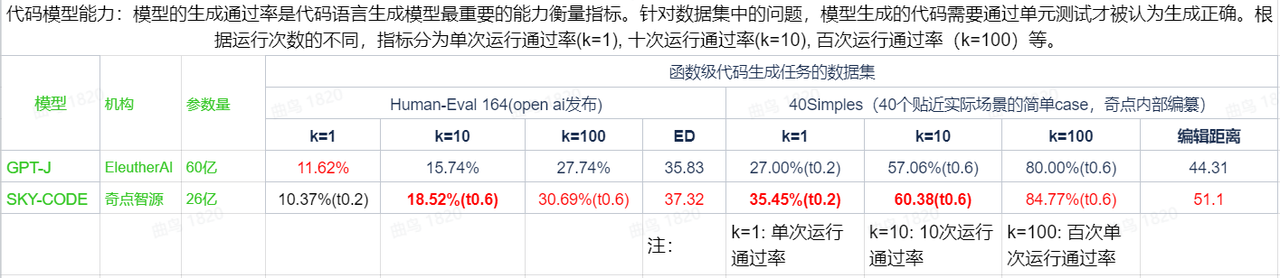
昆仑万维在此领域也推出了第一款多语言开源编程大模型天工智码SkyCode,能够根据代码注释写代码(解题)等,还支持根据中文注释来序列代码。目前市面上的多种主流代码语言(java, javascript, c, c++, python, go, shell)等都得到了支持,该模型可以说是大大提高了写代码的效率,恐怕不久的将来,程序员只需要review代码就OK了。而且生成代码量的速度可以达到每百字的输出,下表对比了 Sky-code 模型与其他代码生成模型的性能:
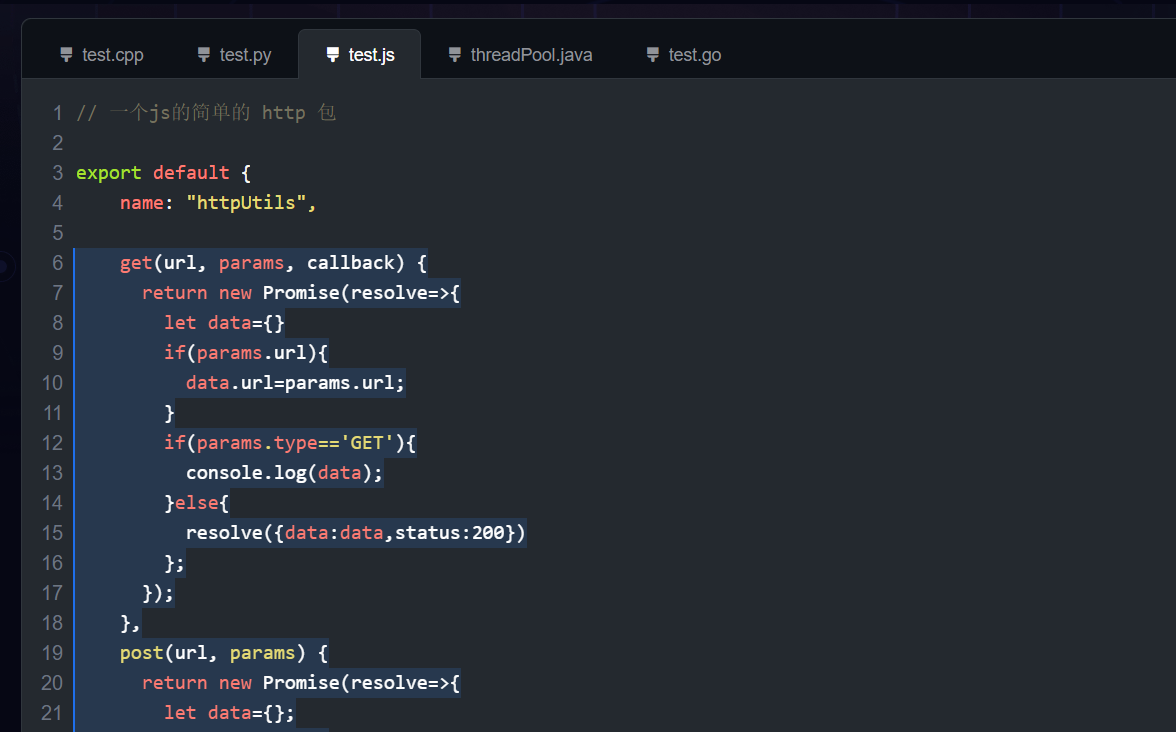
模型生成的js代码:
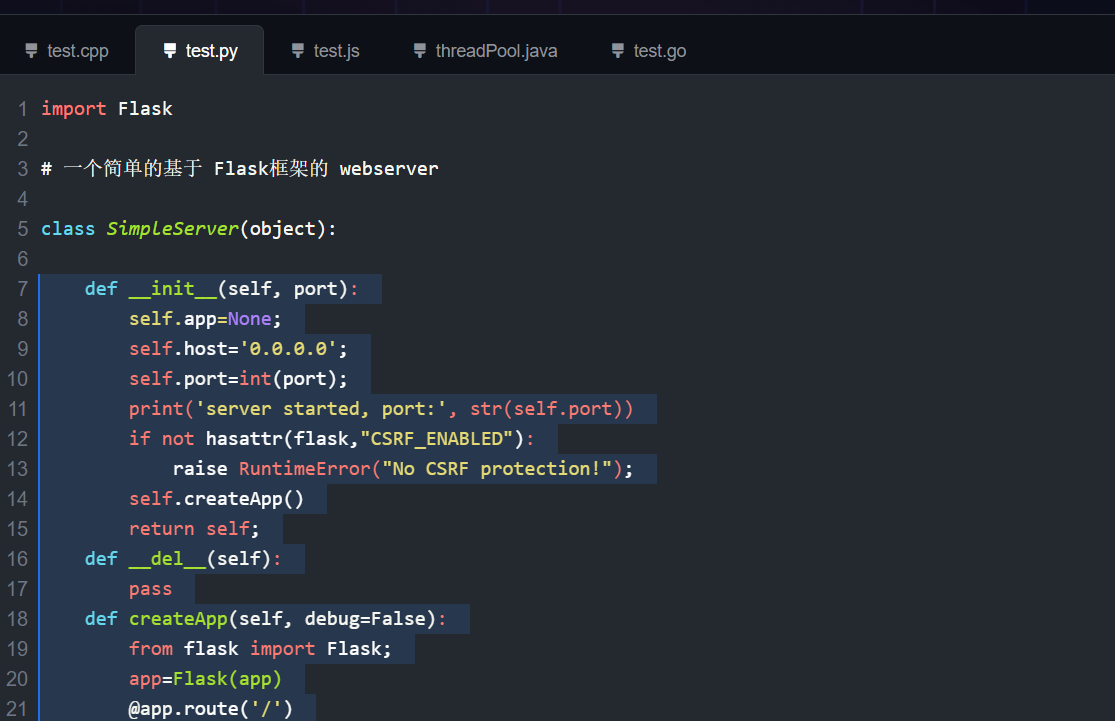
模型生成的Python flask代码:
现阶段天工智码SkyCode支持Visual Studio Code插件扩展,我们可以在扩展中搜索skycode进行安装使用,具体的使用教程可以参考官网的插件使用引导:
未来它们还会陆续支持 Visual Studio, Neovim, JetBrains 等一系列的IDE和编辑器。
五、总结
“昆仑天工”是由昆仑万维集团与合作伙伴奇点智源推出的全系列AIGC模型与算法,昆仑万维作为中国领先的互联网平台出海企业,逐渐在全球范围内形成了海外信息分发及元宇宙平台Opera、海外社交娱乐平台StarX、全球移动游戏平台Ark Games、休闲娱乐平台闲徕互娱、投资板块等五大业务,市场遍及中国、东南亚、非洲、中东、北美、南美、欧洲等地,为全球互联网用户提供社交、资讯、娱乐等信息化服务。截至2022年上半年,全球平均月活跃用户近 4 亿, 海外收入占比达 75%。昆仑万维于2015年登陆创业板,集团旗下的业务和子公司已先后拓展至美国、俄罗斯、日本、韩国、印度,以及欧洲、非洲、东南亚等地的其他国家。
2022年可以说是AIGC的元年,AIGC的时代也从此刻到来。AIGC 作为 UGC 后新一类创作方式,是数智时代的典型应用创新,它的快速发展不仅正在革新数字文化创作的生产范式,也在改变用户与人工智能的交互模式。当然,它现在还处于发展的初期,还有很多的问题等着去解决,还有不明确的未知需要去探索、踩坑。但相信在不久的将来,在高速发展的今天,在技术进步的推动下,在商业前景大好的前提下,AIGC 也将拓展出更多应用方式,更好地服务人们的生活。如 ChatGPT 一样的 AIGC 产品,终将越来越频繁地出现在我们的社会场景之中,成为常态。