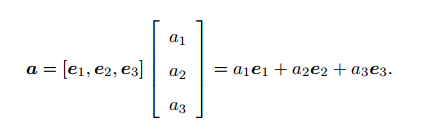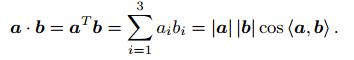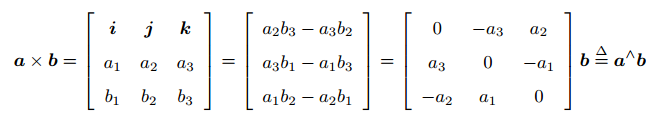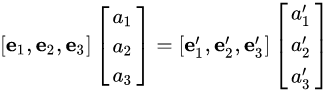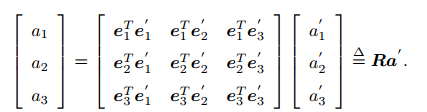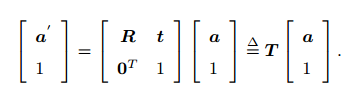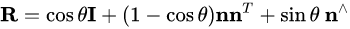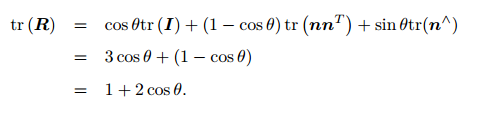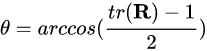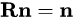三维空间刚体运动
一、向量
1、在描述旋转矩阵前我们先明确向量这个概念。向量是空间中的一个具体实物且不和任何实数相关联。为了描述向量,应该先确定一个具体的坐标系,明确该坐标系的线性基后才能够确定一个向量在该坐标系下的坐标,一个线性空间的基(e1,e2,e3),向量 a表示为(a1,a2,a3)是这向量在这组基下的坐标:
2、向量内积
3、向量外积
外积的方向垂直与这两个向量,大小为 |a||b|sin<a,b>。
^称之为反对称符号。引入侧概念可以将向量外积变成线性运算。
二、旋转 、变换矩阵
2.1、欧式变换:
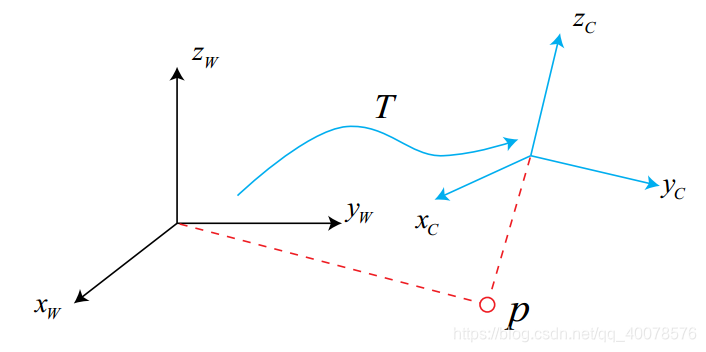
假设存在两个坐标系:一个世界坐标系,定义为某个墙角和它的三条边,并是一个惯性系;一个机器人坐标系,是一个随机器人移动的坐标系。假设机器人观察到了某个向量 [公式] , 它在这两个坐标系中分别有一套坐标。前面说了,向量是一个客观存在的实体,那么必然有一个关系能够将这两套坐标联系起来。
这个关系就是欧式变换。因为机器人的运动是一个刚体运动,所以同一个向量在不同坐标系下的模长和方向都不会发生变化。这样一个欧式变换就是由一个旋转和一个平移两部分组成。先说旋转。
2.1、旋转矩阵
我们先考虑旋转。对于向量P ,他并不会随着坐标系的旋转而发生运动,它在两个坐标系下的表示是相等的:
(e1,e2,e3)和 (e1,e2,e3`) 是连个坐标系的正交基。
R表示为旋转矩阵,旋转矩阵的约束为必须为正交矩阵,||R||=1
2.2、旋转加平移:
** a’ = R-1*a + t= R_t * a + t**
2.3 变换矩阵与齐次坐标
若下式的左边坐标最后一项不为1,强制为1,则a也要跟着变化转化为非齐次坐标(一个点一个唯一表示)
这样子很容易用符号表示出旋转和平移的变换了。
三、旋转向量和欧拉角
3.1、旋转向量
因为旋转矩阵R有九个元素,只表达了3个自由度(三个轴方向的旋转),看起来冗余了,所以人们找到一种更精简的方式来描述旋转。
接下来介绍旋转向量,任意旋转都可以用一个旋转轴和一个旋转角来描述。那么,我们可以用一个向量,其方向为旋转轴n的方向,大小则为旋转角θ ,这种向量就是旋转向量,表示为θn . 前面说到,外积可以用来表示旋转就是因为外积可以用来表示旋转向量:考虑两个不平行的向量a和 b,在右手法则下,用右手的4个指头从a 转向 b ,大拇指的朝向就是旋转向量的方向,即 a x b的方向,而它的大小则由 a 和 b的夹角决定。
旋转向量和旋转矩阵的转换可以用罗德里格斯公式表示:
反之则有
上边的公式推导,不难。
而旋转轴上的向量在旋转后不发生改变,所以:
所以n是R的特征值为1时的特征向量。
四、欧拉角万向死锁问题

具体看博文:
https://www.zhihu.com/question/47736315